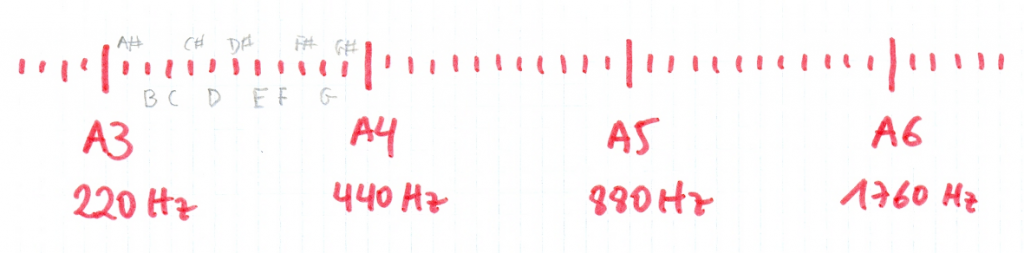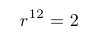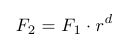Etiqueta: teoría musical

Cálculo de la frecuencia de nuestras notas musicales

Objetivo: entender las matemáticas que hay detrás de un sistema con temperamento igual y aprender a calcular la frecuencia de las notas musicales.

La música y las matemáticas han estado siempre íntimamente ligadas. Conocer la evolución de la concepción musical a lo largo de los siglos, hasta alcanzar el sistema de doce notas con temperamento igual que empleamos en el mundo occidental, es una apasionante aventura, no sólo en sus vertientes musical y matemática, sino también desde las perspectivas cultural, física, técnica y artesanal.

En el artículo de hoy explicaremos qué entiende un matemático por sistema igualmente temperado, conocimiento que nos permitirá calcular con facilidad la frecuencia de cualquier nota de nuestro sistema musical.

A estas alturas del cuento supongo que ya sabrás que nuestro sistema musical tiene doce notas, y no siete. Si no lo tienes claro, echa un vistazo a cualquier imagen de un piano y presta atención a esas teclas negras situadas estratégicamente entre las blancas.

También supongo que sabes que ese patrón de doce notas vuelve a repetirse, encontrando las mismas notas, una octava más agudas a la derecha o más graves a la izquierda. Y que la frecuencia de una nota una octava más aguda que otra es exactamente el doble de esta. Por ejemplo, si tenemos un LA a 440 Hz, el siguiente LA más agudo estará exactamente a una frecuencia de 880 Hz, mientras que el anterior, más grave, se situará en la mitad, 220 Hz.

Esta proporción 2:1 es la única que necesitamos para proseguir con los cálculos que realizaremos a continuación.

He dibujado un piano especial en el que he indicado la frecuencia de unos cuantas notas LA. Es un piano peculiar porque me he permitido poner al mismo nivel las teclas blancas y las negras, de modo que resulte más visual lo que pretendo explicar. He empleado la notación anglosajona a la hora de designar las notas porque me resultaba más cómodo en el gráfico, al ocupar menos espacio.

En vez de ser una visión típica con octavas de DO a DO, he marcado las notas LA como referencia visual, ya que conocemos la frecuencia de una de ellas: la nota LA por encima del DO central tiene una frecuencia exacta de 440 Hz, el sonido de referencia recomendado internacionalmente para la afinación de los instrumentos.

He denominado a esta nota A4 (LA 4), aunque quizás puedas preferir llamarla A3, si eres partidario del sistema franco-belga. Es simplemente una cuestión de elección personal.

Como ya sabemos la relación 2:1 entre octavas, he marcado también las notas A5 y A6, más agudas, y A3, más grave, con sus respectivas frecuencias, inmediatamente calculables multiplicando o dividiendo entre dos.

He colocado también, más pequeñas y en lápiz, el resto de las notas musicales entre A3 y A4. No lo he hecho en las demás octavas para no emborronar demasiado el gráfico.

Imagina que ese dibujo representa un eje de coordenadas en el que se representa la frecuencia de cada nota musical.

¿Es lineal esa representación? Obviamente, no. Si te fijas, la separación entre el A3 y el A4 es de 220 Hz, mientras que entre el A4 y el A5 es del doble, 440 Hz. A su vez, entre A5 y A6 nuevamente el doble, 880 Hz. Sin embargo, sobre el papel, hay la misma distancia entre A3 y A4, que entre A4 y A5 o A5 y A6.

Este tipo de series en las que no hay linealidad, sino proporción constante, se denominan, en matemáticas, progresiones geométricas. Para reducirlas al plano lineal recurrimos a los logaritmos. Gracias a ellos podemos representar linealmente magnitudes que varían exponencialmente. La imagen de las notas uniformemente espaciadas a lo largo de un piano no es más que una visión logarítmica de esta progresión geométrica.

Y lo bueno del asunto, y verdadera clave para comprender lo que es un sistema de temperamento igual, es que la frecuencia de cada una de esas 12 subdivisiones que hay entre medias, correspondientes a cada nota musical, también sigue una representación logarítmica.

Desde el punto de vista matemático, decir que un sistema de doce notas tiene temperamento igual no es otra cosa sino decir que la proporción entre una nota cualquiera y la siguiente (un semitono más alta) es siempre constante.

Hay un factor multiplicativo constante. Si somos capaces de descubrir ese número mágico estaremos en condiciones de poder calcular la frecuencia de cualquier nota.

Calculemos el número que sostiene a nuestro preciado sistema musical. Si A4 es 440 Hz, la siguiente nota, un semitono más alta, LA sostenido (o Si bemol, según prefieras), tendrá por frecuencia:

A su vez, la frecuencia de la nota siguiente, SI, será:

Después de B4 comienza la siguiente octava con C5:

Y así hasta llegar a A5, una octava más alta, doce semitonos, que A4:

Ahora bien, la frecuencia de A5 ya la conocemos, 880 Hz, doble de 440 Hz:

con lo que

Ya tenemos la razón buscada:

Podemos determinar la frecuencia de cualquier nota si conocemos la distancia d en semitonos que la separa de A4:

No es necesario referenciar siempre contra A4; nos sirve cualquier frecuencia conocida, siendo d, en este caso, la distancia en semitonos entre la buscada y la conocida:

Realicemos un ejercicio práctico. Vamos a calcular la frecuencia de MI 5, a una quinta justa por encima de A4. Si contamos, la separación en semitonos entre ambas notas es 7, de modo que:

¿Cuál es la frecuencia del DO central, que se halla nueve semitonos a la izquierda del LA 4? Es un ejemplo en el que d es una distancia negativa.

También podríamos haber resuelto este problema tomando como referencia A3 (220 Hz) y contando tres semitonos hacia delante:

Como vemos, el resultado es el mismo en ambos casos.

Visitaremos en más ocasiones el lado matemático de la música. ¿Sabías que algo que damos por obvio como que Do sostenido tiene la misma frecuencia que Re bemol, es debido a naturaleza igualmente temperada de nuestro sistema musical?

Te dejo pensándolo…

Javier Montero Gabarró

Cálculo de la frecuencia de nuestras notas musicales

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice completo de artículos sobre armonía.

Tal vez te interese...

Escalas: pasar de la fórmula absoluta a la relativa y viceversa

Objetivo: dada una escala en forma absoluta, ser capaz de expresarla relativamente y viceversa.

A la hora de aprender una determinada escala conviene que hagamos el esfuerzo en aprender tanto su fórmula absoluta como la relativa. El proceso de interiorización será mucho más rápido cuando contemplemos la escala desde ambas perspectivas, como veremos.

Propongo para hoy una serie de ejercicios de conversión: dada la fórmula absoluta calcularemos la relativa y, al contrario, partiendo de la fórmula relativa determinaremos la absoluta.

Ejercicio 1

La escala Lidia tiene por fórmula absoluta:

T – T – T – S – T – T – S

¿Cuál es su fórmula relativa?

Seguiremos el siguiente procedimiento:

1) Calcularemos las notas partiendo de Do como tónica.

2) Compararemos las notas resultantes con la escala de Do mayor.

Comenzamos por el primer paso (si tienes problemas calculando tonos y semitonos, revisa los primeros artículos de la categoría Teoría Musical):

Do + T = Re
Re + T = Mi
Mi + T = Fa#
Fa# + S = Sol
Sol + T = La
La + T = Si
Si + S = Do –> Tendríamos un problema si no hubiéramos terminado nuevamente en Do

Comparemos ahora ambas escalas:

Do mayor –> Do – Re – Mi – Fa – Sol – La – Si
Do lidia –> Do – Re – Mi – Fa# – Sol – La – Si

Todas las notas son idénticas, a excepción del cuarto grado, que está sostenido.

La fórmula relativa es, por lo tanto:

Lidia –> 1 – 2 – 3 – #4 – 5 – 6 – 7

Ejercicio 2

La escala menor armónica tiene por fórmula absoluta

T – S – T – T – S – X – S

Determinar la fórmula relativa.

Calculemos las notas partiendo desde Do. Ten en cuenta que con la X estoy designando un intervalo de tono y medio (tres semitonos).

Do + T = Re
Re + S = Mib
Mib + T = Fa
Fa + T = Sol
Sol + S = Lab
Lab + X = Si
Si + S = Do

Comparamos Do mayor con Do menor armónica:

Do mayor –> Do – Re – Mi – Fa – Sol – La – Si
Do menor armónica –> Do – Re – Mib – Fa – Sol – Lab – Si

Todo igual a excepción del tercer y sexto grado, que son bemoles.

Menor armónica –> 1 – 2 – b3 – 4 – 5 – b6 – 7

La operación inversa tampoco entraña ningún misterio.

Ejercicio 3

La escala mixolidia tiene por fórmula relativa

1 – 2 – 3 – 4 – 5 – 6 – b7

¿Cuál es su expresión absoluta?

El procedimiento es el contrario del anterior:

1) Calcularemos las notas comparando la escala con Do mayor.

2) Determinaremos a mano la distancia entre cada nota y la siguiente.

Puesto que sabemos la fórmula relativa, las notas de la escala con tónica en Do son inmediatas:

Do mixolidia –> Do – Re – Mi – Fa – Sol – La – Sib

Observa que hemos hecho bemol el séptimo grado.

Las distancias entre cada par de notas consecutivas son:

Do – Re –> T
Re – Mi –> T
Mi – Fa –> S
Fa – Sol –> T
Sol – La –> T
La – Sib –> S

y, para cerrar, la distancia de la vuelta a Do

Sib – Do –> T

Recopilamos todas esas distancias, obteniendo la fórmula absoluta de la escala mixolidia:

Mixolidia –> T – T – S – T – T – S – T

Ejercicio 4

La escala Dórica b2 tiene por fórmula relativa

Dórica b2 –> 1 – b2 – b3 – 4 – 5 – 6 – b7

¿Cuál es la fórmula absoluta?

Utilizando la fórmula, la escala Do dórica b2 es:

Do dórica b2 –> Do – Reb – Mib – Fa – Sol – La – Sib

Calculemos las distancias:

Do – Reb –> S
Reb – Mib –> T
Mib – Fa –> T
Fa – Sol –> T
Sol – La –> T
La -Sib –> S
Sib – Do –> T

Dórica b2 –> S – T – T – T – T – S – T

Aritmética simple.

Asegúrate de comprender estos ejemplos, te ayudarán a seguir sin problemas la exposición sistemática de escalas que comenzaremos en breve.

Javier Montero Gabarró

Escalas: pasar de la fórmula absoluta a la relativa y viceversa

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice completo de artículos sobre armonía.

Tal vez te interese...

La fórmula relativa de una escala musical

Objetivo: presentar la fórmula relativa y su utilidad práctica para el conocimiento de las diversas escalas musicales.

En un artículo anterior definimos la fórmula absoluta de una escala como aquella que indicaba su composición relacionando cada grado con el anterior. Conocida la fórmula absoluta, la determinación de los grados que constituyen la escala era una cuestión de aritmética simple, como ilustramos en los ejemplos prácticos.

Pero hay más maneras de referirnos a la estructura de una escala musical. La fórmula relativa, que explicaremos a continuación, es esencial para tener una visión clara de cómo es una escala, facilitando además su memorización.

Comencemos por nuestra querida escala mayor en su expresión más sencilla: Do mayor

Do – Re – Mi – Fa – Sol – La – Si – Do

en la que Do es el primer grado, Re el segundo, Mi el tercero, y así sucesivamente.

Indiquemos estos grados por sus números:

1 – 2 – 3 – 4 – 5 – 6 – 7 – 8

Voy a elegir ahora otra escala. Por ejemplo, imagina que te digo que la escala Do lidia está compuesta por las siguientes notas:

Do lidia –> Do – Re – Mi – Fa# – Sol – La – Si – Do

Vamos a comparar ahora Do lidia con Do mayor, grado a grado:

Do – Re – Mi – Fa – Sol – La – Si

Do – Re – Mi – Fa# – Sol – La – Si

Si observas ambas escalas, te darás cuenta de que todos los grados de la escala lidia son los mismos que la de la escala mayor, salvo el cuarto grado, que en aquella es Fa# y en esta Fa natural.

Esto lo podemos indicar así, aumentando un semitono el cuarto grado:

1 – 2 – 3 – #4 – 5 – 6 – 7

Esta es precisamente la fórmula relativa de la escala Lidia y con ella veremos que podremos calcular sus notas en cualquier tonalidad.

La denominamos relativa porque resulta de una comparación con otra escala: la escala mayor. Más adelante veremos que, en ocasiones, resulta útil conocer también la fórmula relativa respecto a otras escalas además de la mayor. Pero, de momento, cuando no matice nada concreto, siempre que me refiera a la fórmula relativa, me estaré refiriendo a la fórmula relativa a la escala mayor.

Quiero recalcar una vez más la cuestión de la terminología. Hay otros músicos que emplean unos términos distintos para referirse a lo mismo, pero, independientemente del sistema al que te adhieras, lo realmente importante es comprender los conceptos que subyacen.

Un nuevo ejemplo: la escala Do menor natural tiene las siguientes notas:

Do menor natural –> Do – Re – Mib – Fa – Sol – Lab – Sib – Do

¿Cuál es la fórmula relativa de la escala menor natural?

Si comparas uno a uno todos los grados respecto a Do mayor, observarás que coinciden todos excepto el tercero, sexto y séptimo, que son bemoles. Por lo tanto, la fórmula relativa es:

Menor natural –> 1 – 2 – b3 – 4 – 5 – b6 – b7

Ya sabes lo que son, entonces, las fórmulas absoluta y relativa de una escala. En el próximo artículo de esta serie realizaremos numerosos ejemplos prácticos variados que te ayudarán a afianzar estos importantes conceptos.

Javier Montero Gabarró

La fórmula relativa de una escala musical

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice completo de artículos sobre armonía.

Tal vez te interese...

La fórmula absoluta de una escala musical

Ha llegado el momento de que comencemos a sumergirnos en el fascinante mundo de las escalas musicales. ¿Te suena a chino si te pregunto por una escala Dórica o por una Lidia b7? ¿Te pierdes cuando te «sacan» de una pentatónica menor?

No te preocupes. En los próximos artículos iremos desentrañando gradualmente todos los misterios de la construcción de escalas. Como suele suceder con casi todo, te darás cuenta de que el asunto es mucho más sencillo de lo que aparenta. Los más temidos fantasmas se desvanecen cuando los iluminas.

Pero antes necesitamos algo de terminología y hoy quiero presentarte el concepto de fórmula absoluta de una escala (en oposición al de fórmula relativa, que trataremos más adelante). Una advertencia: esta terminología es la que yo utilizo y emplearé coherentemente a lo largo de toda la serie; no tiene por qué coincidir con la usada por otros músicos. Lo realmente importante es que sepamos de qué estamos hablando más que el nombre que empleemos para referirnos a ello.

Aunque, eventualmente, podré usar los nombres de las notas propias de nuestro sistema musical (Do, Re, Mi…), recurriré con frecuencia a la notación anglosajona por cuestiones de comodidad. En caso de dudas no estaría mal que hicieras clic sobre el enlace para refrescar conceptos.

Realmente, ya sabes lo que es fórmula absoluta de una escala. Te la presenté en el artículo La fórmula secreta de la escala mayor, que te recomiendo que releas antes de seguir. Cuando hablo de fórmula absoluta, me estoy refiriendo precisamente a esa fórmula secreta.

Una fórmula absoluta de una escala no es más que aquella en la que se detalla la distancia en semitonos de cada grado respecto al anterior.

Antes de que alguien me conteste que, si estamos relacionando cada grado relativamente con el anterior, deberíamos llamarla fórmula relativa, diŕe que, evidentemente, es cierto. No obstante, el absolutismo al que me refiero es que no comparo esa escala con ninguna otra, sino simplemente miro en sí misma. Me reservo el término fórmula relativa para cuando estemos comparando dos escalas entre sí. Pero todo a su momento…

Entonces, ya sabes tu primera fórmula absoluta: la de la escala mayor:

Escala mayor: T – T – S – T – T – T – S

que también podrías escribir como:

2 – 2 – 1 – 2 – 2 – 2 – 1

En la que el 1 hace referencia al semitono y el 2 al tono, puesto que un tono son dos semitonos.

Lo fascinante de todo esto es que, conocida la fórmula de una escala, puedes conocer su composición en cualquier tonalidad sin más que realizar un conteo básico de tonos y semitonos. Léete el artículo antiguo La escala mayor en cualquier tonalidad, en el que se detalla todo el proceso aplicado a un tipo de escala en particular: la escala mayor.

Ya has dado el primer paso. Te aseguro que el camino será llano y sin baches, pero tendrás que ir asimilando cada artículo gradualmente. Merece la pena: conocer lo que hay detrás de las escalas, al igual que de los acordes, cambia radicalmente la forma en la que te relacionas con la música y con los demás músicos.

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2012/05/la-formula-absoluta-de-una-escala-musical/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Tal vez te interese...

Intervalos sin secretos – Ejercicios resueltos IV

Voy a explicarte hoy una técnica avanzada, pero considerablemente más rápida, para el cálculo de intervalos musicales. Para poder beneficiarte con ella deberás tener cierto nivel de familiarización con las notas que constituyen las distintas tonalidades mayores.

¿Qué quiero decir con esto?

Que si, por ejemplo, hablo de Re mayor, de un plumazo, y sin pensar, sepas que las notas de la escala son:

RE – MI – FA# – SOL – LA – SI – DO# – RE

o, si digo Si bemol mayor, sepas que sus notas son

SIb – DO – RE – MIb – FA – SOL – LA – SIb

Los músicos solemos aprehender esto a fuerza de utilizar las tonalidades, más que mediante memorización pura y dura. Cuando tocamos una pieza en Mi mayor ya sabemos qué notas son las que con mayor probabilidad nos aparecerán, así como la familia de acordes que tendremos que usar al armonizar. Ya sabemos que las notas DO que aparezcan probablemente serán sostenidas y que el acorde sobre ese grado, el sexto, será un Do sostenido menor, o que el grado de dominante es un SI natural. Sabemos, también, inmediatamente, cuando una nota o acorde está fuera de esa familia, indicándonos que algún tipo de fenómeno musical está sucediendo en ese instante. A medida que tocamos y tocamos piezas distintas en Mi mayor vamos familiarizándonos más profundamente con la tonalidad.

Si aún no estás en ese punto, no te preocupes, será una evolución natural. Entre tanto, sigue perfeccionando la construcción de escalas en cualquier tonalidad.

Un punto intermedio es aquel en el que la construcción de escalas no es inmediata, pero casi lo es. Puede que ya sepas que Re mayor tienes dos alteraciones, tres La mayor y cuatro Mi mayor, aunque necesites ponerte a pensar un poco para localizar los grados exactos en los que están. En este sentido, conocer el círculo de quintas ayuda bastante: la hora de reloj en la que está posicionada la nota indica cuántos sostenidos tiene su armadura. Visto por la izquierda, como si se tratase de un reloj que girara en sentido contrario, obtendríamos, de modo similar, el número de bemoles de la armadura. MI está a las «cuatro de la tarde», luego Mi mayor posee, en su armadura, cuatro notas alteradas.

Hablaremos largo y tendido del círculo de quintas en estas series. Vayamos ahora con el método para calcular intervalos.

El método parte de un concepto fundamental que ya tratamos en la segunda entrega de Intervalos sin secretos: en relación a la tónica, todos los intervalos de una escala mayor son mayores o perfectos.

Con esta idea en mente, la metodología consiste en tomar como referencia la escala mayor de la primera nota del intervalo y encajar después la segunda nota en esa escala para determinar la amplitud y cualidad del intervalo.

Lo veremos claramente en los siguientes ejercicios prácticos.

Ejercicio 5

Determinar el intervalo formado por los siguientes pares de notas:

a) RE y FA#
b) SIb y MI
c) LA y FA

Solución

a) Comenzamos desplegando la escala de la primera nota. Esto sucede en la mente, pero lo escribimos aquí para ilustrar la técnica:

RE – MI – FA# – SOL – LA – SI – DO# – RE

La nota destino, FA#, está en esa escala, sobre el grado 3, luego el intervalo buscado es una tercera mayor, ya que todos los intervalos de la escala mayor, como hemos dicho, son mayores (segundo, tercer, sexto y séptimo grados) o perfectos (primero, cuarto, quinto y octavo grados).

b) La escala de Si bemol mayor es

SIb – DO – RE – MIb – FA – SOL – LA – SIb

La nota buscada, MI, no está en la escala, sino que, en su lugar, figura MI bemol, que estaría a una cuarta perfecta (o justa). Para pasar de MI bemol a MI hay que aumentar un semitono. Ya sabemos, por el modelo del muelle, que si a un intervalo perfecto lo hacemos crecer un semitono obtenemos un intervalo aumentado.

Por lo tanto, si una cuarta justa la aumentamos un semitono, obtenemos una cuarta aumentada, que es la distancia entre SI bemol y MI.

c) Construimos La mayor:

LA – SI – DO# – RE – MI – FA# – SOL# – LA

El FA de la escala es sostenido, y no natural. Habrá que bajar un semitono. Si a una sexta mayor le quitamos un semitono obtenemos, según el modelo del muelle, una sexta menor.

Ejercicio 6

a) Calcular qué nota es una séptima menor por encima de Re.
b) ¿Y una tercera mayor por debajo?

Solución

a) No vamos a escribir ya la escala (pero tú hazlo si no lo ves claro). El śeptimo grado de Re mayor es DO sostenido, que forma un intervalo de una séptima mayor respecto a RE. Como nos piden una séptima menor, habrá que quitarle un semitono. La respuesta es, por lo tanto, DO natural.

b) Ya sabemos por las secciones teóricas que una tercera mayor por debajo tiene el mismo nombre de nota que una sexta menor por arriba, pues la suma de un intervalo más su inversión suman 9, y la inversión de un intervalo mayor es otro menor.

El sexto grado de la escala de Re mayor es SI, que está a una distancia de una sexta mayor. Una sexta menor, por lo tanto, es SI bemol que es la tercera mayor descendente buscada.

Es muy interesante que practiques este método de cálculo. Es un buen ejercicio con el que matarás dos pájaros de un tiro: agilidad en la determinación de notas de una escala y en el cálculo de intervalos.

Intervalos sin secretos – Ejercicios resueltos IV

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Tal vez te interese...

Intervalos sin secretos – Ejercicios resueltos III

Una vez dominada la metodología fundamental, vamos a dedicar este tercer lote de ejercicios a la resolución de problemas que pueden simplificarse empleando las propiedades de los intervalos que ya tratamos en la sección teórica.

El primer ejemplo ilustra el caso en el que los intervalos son de amplitud superior a la mitad de la escala (de quinta en adelante). Veremos un método que facilitará su cálculo.

Ejercicio 3

a) ¿Qué intervalo existe entre RE y SI bemol?
b) En el acorde E7 (MI séptima). ¿Qué nota es la séptima? (Observación: En los acordes de séptima, la séptima es una séptima menor?

Solución

a) Las propiedades que aplicaremos son las siguientes:

P1) La amplitud de un intervalo más la de su inversión suman nueve.

P2) La inversión de un intervalo justo sigue siendo un intervalo justo; la inversión de un intervalo mayor da otro menor y viceversa; la inversión de un intervalo aumentado genera otro disminuido y viceversa.

¿Cómo se aplica esto a nuestro problema en particular?

Al tratarse de una distancia más corta, resulta más sencillo calcular la distancia entre SI bemol y RE, inversión de RE y SI bemol.

SI – DO – RE –> es una tercera

Contemos ahora los semitonos:

SIb – SI(1) – DO(2) – DO#/REb(3) – RE(4)

Si consultamos la tabla de referencia, comprobamos que una tercera compuesta de 4 semitonos es una tercera mayor.

Aplicando las propiedades, ¿cuál es la inversión de una tercera mayor?

Comencemos por la amplitud. Por P1 sabemos que deben sumar nueve, por lo que se trata de una sexta (6+3=9).

Como el intervalo es mayor, su inversión será menor. Por lo tanto, la distancia entre RE y SI bemol es una sexta menor.

b) ¿Cuál es la inversión de una séptima menor? Por P1 y P2 sabemos que la respuesta es una segunda mayor.

Por lo tanto, una séptima menor por encima de MI está la misma nota que una segunda mayor por debajo (salvo que entre ambas hay una octava de diferencia).

Es más rápido contar una segunda mayor hacia atrás que una séptima menor hacia delante.

Una segunda hacia atrás es MI – RE –> RE

Calculemos si se trata de un RE natural o alterado.

Por la tabla de referencia sabemos que una segunda mayor son dos dos semitonos. Contando hacia atrás:

MI – MIb/RE#(1) – RE(2)

Conclusión: la séptima menor del acorde E7 es RE.

En el ejercicio siguiente trataremos intervalos cuya amplitud supera la octava.

Ejercicio 4

¿Qué nota es la decimo primera aumentada por encima de SOL?

Solución

Si recuerdas el desarrollo teórico, todo intervalo que excede de la octava es equivalente (pero una octava más agudo) al que se obtiene sustrayendo siete de la amplitud.

Es decir, un intervalo de novena es equivalente a uno de segunda (9-7=2), uno de décima a uno de tercera, etc.

Por lo tanto, una 11A es equivalente (una octava más aguda) a una 4A (11-7=4).

Ya sabemos calcular una cuarta aumentada:

Es una cuarta; contando

SOL – LA – SI – DO

Consultando la tabla, una cuarta aumentada es equivalente a 6 semitonos.

SOL – SOL#/LAb(1) – LA(2) – LA#/SIb(3) – SI(4) – DO(5) – DO#/REb(6)

Como ha de ser un DO, la respuesta es DO#.

Date cuenta de que el truco del ejercicio anterior no habría sido especialmente práctico. Seis semitonos (el tritono) caen justo en la mitad de la escala cromática (12 semitonos): es lo mismo contar 6 semitonos hacia adelante que seis semitonos hacia atrás, no ganaríamos nada invirtiendo el intervalo.

En la próxima entrega explicaré una técnica avanzada para el cálculo de intervalos muy útil para los que ya están familiarizados con las diferentes tonalidades.

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2012/04/intervalos-sin-secretos-ejercicios-resueltos-iii/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Tal vez te interese...

Construcción de acordes – 12: Séptima mayor con quinta aumentada

Doce entregas ya. A estas alturas uno debe saber «fabricar» ya casi cualquier acorde.

El nombre del que nos ocupa hoy habla por sí solo: como no se especifica que el acorde sea menor ni disminuido, la tercera debe ser mayor. Por el título, sabemos que la quinta es aumentada y la séptima mayor.

La fórmula debe resultar evidente:

7M(#5) –> 1 – 3 – #5 – 7

También puedes encontrártelo escrito como maj7(#5), +(7M), aug(7M), o con el símbolo del triángulo en vez de la séptima mayor (notación típica de jazz). Que no te confundan las distintas variantes a la hora de nombrar un mismo acorde.

Si te cuestionas la utilidad de este acorde, con sonoridad un tanto extraña, debes saber que aparece sobre el tercer grado cuando armonizas la escala menor armónica. Si lo que te he dicho no te suena a chino, no estaría mal que lo verificaras (si no es el caso, no te preocupes, pronto dedicaré una serie a la armonización de las escalas principales).

Como siempre, veamos dos ejemplos de cálculo. Si aterrizas por primera vez en esta serie sin haberte mirado los artículos anteriores, consulta, al menos, la primera entrega, en la que se explica la metodología.

Comenzemos por Do séptima mayor con la quinta aumentada, C7M(#5). Como siempre, tomamos como referencia la escala mayor a partir de la fundamental:

C – D – E – F – G – A – B – C

Tomamos los grados indicados en la fórmula, aumentando el quinto:

C7M(#5) –> C – E – G# – B

Otro ejemplo: determinemos las notas de A7M(#5).

La escala de La mayor es:

A – B – C# – D – E – F# – G# – A

por lo que,

A7M(#5) –> A – C# – E#(igual a F) – G#

Date cuenta del detalle: aunque a efectos prácticos hacemos sonar un FA, el nombre real de la quinta aumentada es MI sostenido. Son enarmónicos.

Aún nos quedan muchos acordes por ver; no obstante, la siguiente entrada será especial: prepararé una tabla resumen con todas las fórmulas vistas hasta ahora. Será un artículo dinámico que irá creciendo conforme vaya presentando nuevos acordes.

Javier Montero Gabarró

Construcción de acordes – 12: Séptima mayor con quinta aumentada

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Tal vez te interese...

Intervalos sin secretos: Ejercicios resueltos II

Vamos a dedicar un par de minutos a seguir resolviendo ejercicios sobre intervalos musicales. En la anterior entrega practicamos el cálculo de intervalos una vez especificada las notas inicial y final. En los ejercicios que propongo hoy determinaremos la nota destino conocidos la nota inicial y el tipo de intervalo.

Ejercicio 2

a) ¿Qué nota hay una sexta mayor sobre SI?
b) ¿Qué nota está una tercera menor por debajo de FA?
c) ¿Qué nota está una cuarta aumentada por encima de RE? ¿Y por debajo?

Solución

a) Primero determinemos el nombre de la nota natural destino. Al tratarse de una sexta, debemos contar seis notas, incluyendo los extremos:

SI – DO – RE – MI – FA – SOL

Ya sabemos que estamos ante un SOL, pero, ¿será natural?¿sostenido?¿bemol?

Para responder a esta pregunta necesitamos consultar la tabla de referencia de intervalos para saber de cuántos semitonos se compone la sexta mayor.

Sexta mayor –> 9 semitonos

Volvemos a contar, pero esta vez cromáticamente. Utilizo la notación anglosajona para mayor comodidad, indicando entre paréntesis el número de semitonos respecto al origen.

B – C(1) – C#/Db(2) – D(3) – D#/Eb(4) – E(5) – F(6) – F#/Gb(7) – G(8) – G#/Ab(9)

La cuenta se detiene en SOL # o su enarmónico, LA b. Como tenemos que elegir un SOL, la respuesta es SOL #.

En el próximo artículo veremos un modo mucho más elegante de llegar a la misma conclusión, pero ahora interesa que domines el conteo básico.

b) Esta vez estamos ante un intervalo descendente. La única diferencia es que hay que contar hacia atrás.

FA – MI – RE

Estamos ante un RE, que será natural, sostenido o bemol en función de los semitonos de que se componga el intervalo. Consultando la tabla,

Tercera menor –> 3 semitonos

Contamos cromáticamente hacia atrás,

F – E(1) – D#/Eb(2) – D(3)

La respuesta por tanto es RE (natural, sin alteraciones).

c) Comencemos por el intervalo ascendente.

RE – MI – FA – SOL

Tiene que ser un SOL. Determinemos si es natural, sostenido o bemol.

Cuarta aumentada –> 6 semitonos

D – D#/Eb(1) – E(2) – F(3) – F#/Gb(4) – G(5) – G#/Ab(6)

Con lo que una cuarta aumentada por encima de RE tenemos a SOL #.

¿Y una cuarta aumentada por debajo? Realizamos la misma operación, pero esta vez contando hacia atrás:

RE – DO – SI – LA

D – C#/Db(1) – C(2) – B(3) – A#/Bb(4) – A(5) – G#/Ab(6)

Y así, una cuarta aumentada por debajo de RE está LA bemol.

¿Notas alguna similitud respecto a la respuesta anterior?

SOL sostenido y LA bemol son enarmónicos, es decir, dos notas con nombre diferente pero que corresponden al mismo sonido. ¿Qué curioso, no?

La explicación radica en que una cuarta aumentada (al igual que una quinta disminuida) se compone de 6 semitonos, la mitad justo de los doce semitonos que contiene una octava. Y es lo mismo avanzar la mitad hacia delante que retroceder la mitad hacia atrás, por eso son el mismo sonido.

Ese intervalo de seis semitonos, también conocido como tritono (de tres tonos) cae justamente en mitad de la escala. La inversión de un tritono es el mismo tritono. No es de extrañar que antiguamente se le atribuyeran cualidades diabólicas.

En la tercera entrega veremos una forma elegante de simplificar estos problemas cuando la distancia en semitonos sea mayor de 6. En la cuarta explicaré una técnica más avanzada, útil para los que ya están más familiarizados con las distintas tonalidades.

Javier Montero Gabarró

Intervalos sin secretos: Ejercicios resueltos II

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Tal vez te interese...

Construcción de acordes – 11: menor con séptima mayor

En nuestra incursión por el colorido mundo de los acordes vamos a hacer parada en otra cuatriada básica que debemos conocer: menor con la séptima mayor. Este acorde surge de modo natural sobre el primer grado cuando armonizamos por terceras las escalas menores armónica y melódica. Veamos cómo se construye.

Todo está en su nombre, si somos cuidadosos y no mezclamos los términos mayor y menor: en un acorde menor con la séptima mayor la triada es menor y es la séptima la que es mayor. En cifrado moderno, suele indicarse como m7M, mM7, m(maj7), o cambiando la m de menor por min o por un signo menos (-).

Lo realmente importante es comprender que la cualidad de la séptima es mayor. Lo que es menor es la triada básica. Su fórmula, por lo tanto, no debe suponerte ningún misterio:

m7M: 1 – b3 – 5 – 7

Veamos un par de ejemplos de aplicación de la fórmula. Comencemos por Cm7M.

Siguiendo el método descrito en esta serie, empezamos escribiendo la escala de Do mayor:

C – D – E – F – G – A – B – C

Tomamos a continuación los grados indicados en la fórmula, con lo que

Cm7M –> C – Eb – G – B

Sencillo, ¿verdad? Sabiendo la fórmula podemos construir cualquier acorde.

Un segundo ejemplo: calculemos las notas de Am7M.

La escala de La mayor es la siguiente:

A – B – C# – D – E – F# – G# – A

con lo que

Am7M –> A – C – E – G#

Más de lo mismo.

Merece la pena hacer un esfuerzo y familiarizarse con los acordes y sus fórmulas. Esto nos permitirá diseñar nuevas formas para los acordes que ya conocemos, inversiones, usos imaginativos, o incluso construir acordes desconocidos, ya que sabremos deducir su composición a partir del nombre. Esto es especialmente importante para los guitarristas que, a diferencia de los pianistas, suelen tener una excesiva dependencia visual sobre las formas en el instrumento.

Javier Montero Gabarró

Construcción de acordes – 11: menor con séptima mayor

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Tal vez te interese...

Intervalos sin secretos: Ejercicios resueltos I

Vamos a dedicar un rato a aplicar lo aprendido sobre el cálculo de intervalos en los artículos anteriores (I y II) y resolveremos algunos ejercicios prácticos. En esta primera entrega trataremos algunos ejemplos básicos; en las próximas aplicaremos algunos métodos particulares y técnicas más avanzadas.

Para comprender estos ejercicios necesitamos remontarnos a la tabla de referencia que preparé hace unos días.

Ejercicio 1:

Los siguientes pares de notas delimitan un intervalo ascendente. Indicar de cuál se trata:

a) C – F#
b) A# – C
c) D – C
d) Gb – Db
e) Gb – D#

Solución:

a) Comenzamos calculando la distancia. Contamos sólo las notas naturales, incluyendo ambos extremos:

C – D – E – F

Se trata de una cuarta. Hay que determinar ahora su cualidad, para lo cual debemos contar el número de semitonos de diferencia totales:

C – C#(1) – D(2) – D#(3) – E (4) – F(5) – F#(6)

Seis semitonos (o tres tonos, tritono: el intervalo del diablo).

Consultamos la tabla y encontramos que dentro del grupo de cuartas, la que tiene seis semitonos es la aumentada.

Con lo que C – F# –> Cuarta aumentada

b) Determinemos la distancia:

A – B – C; una tercera.

Contemos semitonos:

A# – B(1) – C(2)

Miramos en la tabla el grupo de terceras y la que tiene dos semitonos es la disminuida:

A# – C –> Tercera disminuida

c) D – E – F – G – A – B – C; una séptima.

D – D#(1) – E(2) – F(3) – F#(4) – G(5) – G#(6) – A(7) – A#(8) – B(9) – C(10)

D – C –> Séptima menor

Más adelante veremos un modo mucho más rápido de llegar a esta conclusión, pero por el momento viene bien entretenerse con el conteo básico.

d) G – A – B – C – D; una quinta.

Gb – G(1) – G#(2) – A(3) – A#(4) – B(5) – C(6) – C#/Db(7) (observa que C# es enarmónico de Db)

Gb – Db –> Quinta justa o perfecta.

e) Al igual que el caso anterior, se trata de una quinta. Pero esta vez la distancia es 9 semitonos.

Gb – G(1) – G#(2) – A(3) – A#(4) – B(5) – C(6) – C#(7) – D(8) – D#(9)

La distancia de 9 semitonos no figura en el cuadro de quintas. ¿Qué intervalo es este?

Es un semitono más que el aumentado. A este tipo de intervalos se los conoce como doble aumentados.

De igual manera, al intervalo un semitono menor que el disminuido se le denomina doble disminuido.

Gb – D# –> Quinta doble aumentada

Date cuenta de que D# es enarmónico de Eb, por lo que, a efectos prácticos, una quinta doble aumentada es enarmónica de una sexta mayor.

Ningún misterio hasta aquí, ¿verdad? ¿Listo para el ejercicio 2?

Javier Montero Gabarró

Intervalos sin secretos: Ejercicios resueltos I

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

Fecha de la última modificación del artículo original: 30 de marzo de 2012

El Club del Autodidacta

Uso de cookies

Este sitio web utiliza cookies para que usted tenga la mejor experiencia de usuario. Si continúa navegando está dando su consentimiento para la aceptación de las mencionadas cookies y la aceptación de nuestra política de cookies, pinche el enlace para mayor información.plugin cookies

ACEPTAR
Aviso de cookies