 Objetivo: presentar el concepto de cent como unidad para comparar frecuencias.
Objetivo: presentar el concepto de cent como unidad para comparar frecuencias.
Para ponernos en situación, comencemos por un breve repaso a las conclusiones que establecimos en en el artículo dedicado a la frecuencia de las notas musicales.
Dividimos cada octava en doce notas, estableciendo una progresión geométrica asociada a la frecuencia de cada una de ellas. A la distancia entre dos notas consecutivas la denominamos semitono.
En términos matemáticos, dada una nota determinada, de frecuencia f, vimos que la frecuencia de cualquier otra, f’, separada una distancia de n semitonos de la primera es:
Dedujimos el valor de r basándonos en el hecho de que en cada octava (12 semitonos) se duplica la frecuencia. Esto es:
Es importante entender que, en cierto modo, el semitono no es más que una magnitud relativa que nos permite comparar la frecuencia de dos notas desde una visión logarítmica lineal, en la que, como en un piano, dividimos físicamente en 12 partes iguales una octava (imaginando que teclas negras fueran semejantes en forma y disposición a las teclas blancas), pese a que la relación de frecuencias es, en realidad, exponencial.
Naturalmente, es una comparación que sólo es práctica cuando la hacemos sobre notas que se han afinado perfectamente entre sí, pero resulta un tanto grosera si queremos comparar, en general, cualquier par de frecuencias.
Para comparar frecuencias con mayor precisión necesitamos disponer de unidades de medida más pequeñas que el semitono, y es aquí donde entra en juego el concepto de cent.
Imagina que cogemos nuestro teclado y dividimos cada tecla en cien microscópicas teclitas. Al intervalo formado entre dos de esas teclitas consecutivas lo denominamos cent.
Eso es equivalente a decir que si antes, en una octava, encontrábamos 12 teclas, en este nuevo piano de teclitas microscópicas nos aparecen ahora 1200.
¿Y qué ocurre con la frecuencia de cada una de esas «micro» notas? Pues que presenta la misma relación matemática que se observa en las teclas grandes: una progresión geométrica. La frecuencia de una «micro» nota es igual a la de la anterior multiplicada por un factor constante.
Para hallar ese factor multiplicativo, nos apoyamos nuevamente en el hecho de que cada octava duplica la frecuencia. De modo que:
Más que entretenernos en calcular cuál sería la frecuencia de cada una de esas micronotas, lo que más nos puede interesar en la práctica es saber cuántos cents hay de diferencia entre dos determinadas frecuencias. Los afinadores electrónicos, por ejemplo, pueden presentarte esta información, indicándote cuantitativamente, además de visualmente, cómo anda de desafinado tu instrumento.
Consideremos dos notas, de frecuencia f y f’, separadas entre sí una distancia de n cents (es decir, entre ambas hay n teclitas de separación en nuestro teclado microscópico).
La progresión geométrica que relaciona ambas frecuencias establece, entonces, que
Despejando n llegamos a la fórmula pretendida:
Como ejercicio práctico, vamos a calcular qué diferencia hay en cents entre un piano afinado a 440 Hz y otro a 432 Hz. Esa es la frecuencia de la nota LA sobre el Do central.
Ten siempre muy presente la imagen visual para entender la magnitud del resultado. Cada 100 cents es el salto de un semitono a otro. En el ejemplo, 32 cents corresponden a 32 teclitas en nuestro teclado microscópico o, aproximadamente, la tercera parte del espacio existente entre dos teclas grandes consecutivas.
Otro ejercicio:
Cuando decidimos optar, en nuestro sistema musical actual, por el temperamento igual tuvimos que sacrificar la consonancia perfecta. Una quinta justa, por ejemplo, ya no obedece a la relación 3:2, sino a la que establece la progresión geométrica de la temperación igual.
¿Cuánto hemos perdido en el reajuste? Dicho de otra forma, ¿cuántos cents de diferencia existen entre la quinta justa pura y la igualmente temperada?
No te será difícil, ahora, realizar los cálculos por tu cuenta…
Javier Montero Gabarró
El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)
El Club del Autodidacta
Índice de todos los artículos de armonía.
Índice de lectura recomendado de la categoría Armonía.

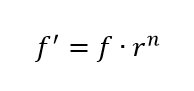
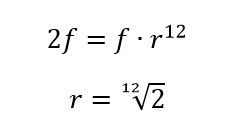
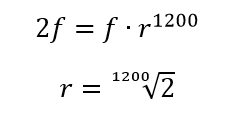

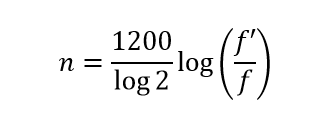
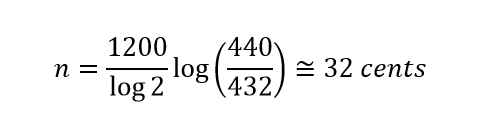
Los cents de diferencia entra una quinta justa pura y temperada es igual a 2 ?
En efecto, Miguel, algo menor que 2 cents, lo que te da una buena idea de lo poco que se ha perdido en relación a los beneficios de un temperamento igual.
Saludos
Jaj! Voy a repasar todo el texto! Saludos y muy bueno el sitio!
Que buena explicación, esperando por más artículos.
Gracias, Martín, aún queda mucho de que hablar.
Saludos
Muy clarito y conciso Martin. Me has sacado de un apuro para un trabajito que necesitaba prepararlo urgente. Gracias