 Objetivo: entender las matemáticas que hay detrás de un sistema con temperamento igual y aprender a calcular la frecuencia de las notas musicales.
Objetivo: entender las matemáticas que hay detrás de un sistema con temperamento igual y aprender a calcular la frecuencia de las notas musicales.
La música y las matemáticas han estado siempre íntimamente ligadas. Conocer la evolución de la concepción musical a lo largo de los siglos, hasta alcanzar el sistema de doce notas con temperamento igual que empleamos en el mundo occidental, es una apasionante aventura, no sólo en sus vertientes musical y matemática, sino también desde las perspectivas cultural, física, técnica y artesanal.
En el artículo de hoy explicaremos qué entiende un matemático por sistema igualmente temperado, conocimiento que nos permitirá calcular con facilidad la frecuencia de cualquier nota de nuestro sistema musical.
A estas alturas del cuento supongo que ya sabrás que nuestro sistema musical tiene doce notas, y no siete. Si no lo tienes claro, echa un vistazo a cualquier imagen de un piano y presta atención a esas teclas negras situadas estratégicamente entre las blancas.
También supongo que sabes que ese patrón de doce notas vuelve a repetirse, encontrando las mismas notas, una octava más agudas a la derecha o más graves a la izquierda. Y que la frecuencia de una nota una octava más aguda que otra es exactamente el doble de esta. Por ejemplo, si tenemos un LA a 440 Hz, el siguiente LA más agudo estará exactamente a una frecuencia de 880 Hz, mientras que el anterior, más grave, se situará en la mitad, 220 Hz.
Esta proporción 2:1 es la única que necesitamos para proseguir con los cálculos que realizaremos a continuación.
He dibujado un piano especial en el que he indicado la frecuencia de unos cuantas notas LA. Es un piano peculiar porque me he permitido poner al mismo nivel las teclas blancas y las negras, de modo que resulte más visual lo que pretendo explicar. He empleado la notación anglosajona a la hora de designar las notas porque me resultaba más cómodo en el gráfico, al ocupar menos espacio.
En vez de ser una visión típica con octavas de DO a DO, he marcado las notas LA como referencia visual, ya que conocemos la frecuencia de una de ellas: la nota LA por encima del DO central tiene una frecuencia exacta de 440 Hz, el sonido de referencia recomendado internacionalmente para la afinación de los instrumentos.
He denominado a esta nota A4 (LA 4), aunque quizás puedas preferir llamarla A3, si eres partidario del sistema franco-belga. Es simplemente una cuestión de elección personal.
Como ya sabemos la relación 2:1 entre octavas, he marcado también las notas A5 y A6, más agudas, y A3, más grave, con sus respectivas frecuencias, inmediatamente calculables multiplicando o dividiendo entre dos.
He colocado también, más pequeñas y en lápiz, el resto de las notas musicales entre A3 y A4. No lo he hecho en las demás octavas para no emborronar demasiado el gráfico.
Imagina que ese dibujo representa un eje de coordenadas en el que se representa la frecuencia de cada nota musical.
¿Es lineal esa representación? Obviamente, no. Si te fijas, la separación entre el A3 y el A4 es de 220 Hz, mientras que entre el A4 y el A5 es del doble, 440 Hz. A su vez, entre A5 y A6 nuevamente el doble, 880 Hz. Sin embargo, sobre el papel, hay la misma distancia entre A3 y A4, que entre A4 y A5 o A5 y A6.
Este tipo de series en las que no hay linealidad, sino proporción constante, se denominan, en matemáticas, progresiones geométricas. Para reducirlas al plano lineal recurrimos a los logaritmos. Gracias a ellos podemos representar linealmente magnitudes que varían exponencialmente. La imagen de las notas uniformemente espaciadas a lo largo de un piano no es más que una visión logarítmica de esta progresión geométrica.
Y lo bueno del asunto, y verdadera clave para comprender lo que es un sistema de temperamento igual, es que la frecuencia de cada una de esas 12 subdivisiones que hay entre medias, correspondientes a cada nota musical, también sigue una representación logarítmica.
Desde el punto de vista matemático, decir que un sistema de doce notas tiene temperamento igual no es otra cosa sino decir que la proporción entre una nota cualquiera y la siguiente (un semitono más alta) es siempre constante.
Hay un factor multiplicativo constante. Si somos capaces de descubrir ese número mágico estaremos en condiciones de poder calcular la frecuencia de cualquier nota.
Calculemos el número que sostiene a nuestro preciado sistema musical. Si A4 es 440 Hz, la siguiente nota, un semitono más alta, LA sostenido (o Si bemol, según prefieras), tendrá por frecuencia:
A su vez, la frecuencia de la nota siguiente, SI, será:
Después de B4 comienza la siguiente octava con C5:
Y así hasta llegar a A5, una octava más alta, doce semitonos, que A4:
Ahora bien, la frecuencia de A5 ya la conocemos, 880 Hz, doble de 440 Hz:
con lo que
Ya tenemos la razón buscada:
Podemos determinar la frecuencia de cualquier nota si conocemos la distancia d en semitonos que la separa de A4:
No es necesario referenciar siempre contra A4; nos sirve cualquier frecuencia conocida, siendo d, en este caso, la distancia en semitonos entre la buscada y la conocida:
Realicemos un ejercicio práctico. Vamos a calcular la frecuencia de MI 5, a una quinta justa por encima de A4. Si contamos, la separación en semitonos entre ambas notas es 7, de modo que:
¿Cuál es la frecuencia del DO central, que se halla nueve semitonos a la izquierda del LA 4? Es un ejemplo en el que d es una distancia negativa.
También podríamos haber resuelto este problema tomando como referencia A3 (220 Hz) y contando tres semitonos hacia delante:
Como vemos, el resultado es el mismo en ambos casos.
Visitaremos en más ocasiones el lado matemático de la música. ¿Sabías que algo que damos por obvio como que Do sostenido tiene la misma frecuencia que Re bemol, es debido a naturaleza igualmente temperada de nuestro sistema musical?
Te dejo pensándolo…
Javier Montero Gabarró
El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)
El Club del Autodidacta
Índice completo de artículos sobre armonía.

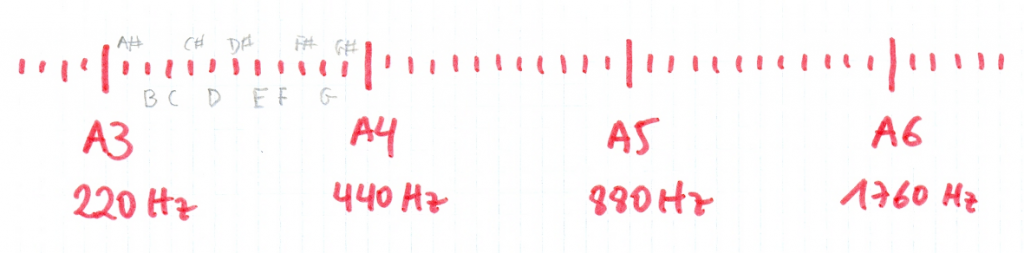
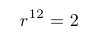
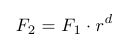


fantastic!!!!!!
Tengo que cal calculas las frecuencias Hertz de cada nota musical con sus medios tonos en la 432 herrz La si alguien me puede ayudar vidaenlinea10@gmail.com gracias de antemano
Multiplica
432 x 1.0594623 = La#
432 x 1.0594623 x 1.0594623 = Si
432 x 1.0594623 x 1.0594623 x 1.0594623 = Do
432 x 1.0594623 x 1.0594623 x 1.0594623 x 1.0594623 = Do#
Y así, hasta llegar a Sol#. para el La de la octava, solo tienes que multiplicar 432 x 2.
Todo esta explicado muy clarito en por Javier.
Debería ser 440Hz x 1.0594623 = La#
te felicito, tenés ALMA y corazón de docente.
Nunca mejor explicado.
¡Gracias por tus palabras, Oriana!
Buen día.
Algo no me cuadra… ¿no se supone que la frecuencia de Mi5 es de 660 Hz? ¿A qué se debe esta inexactitud?
En nuestro sistema musical una quinta no es la relación perfecta 3:2, sino algo menos (1’4983, casi 1,5). Como ejercicio te propongo que recorras el círculo de quintas partiendo desde el La4 multiplicando cada vez por 1,5. Cuando regreses al La, tras haber dado la vuelta completa, te darás cuenta de que no has aterrizado en las siete octavas esperadas, sino que te pasas algo de largo. Para solucionar esto y otros problemas ocasionados por la perfección pitagórica se estableció la división logarítmica propia de nuestro sistema igualmente temperado.
¿Es lo que se llama la «quinta del lobo»?
De todo esto procede la que se denomina «quinta del lobo», en efecto.
Anteriormente, para corregir ese «error» que evitaba que volvieran a coincidir quintas y octavas, se optó por dejar una quinta algo más pequeña que las restantes. Esa era la quinta del lobo.
En nuestro actual sistema bien temperado eso ya no tiene sentido.
Ya, pero, en cambio, las relaciones de frecuencia entre las notas de un acorde no son exactas. O sea que, en realidad, en la escala temperada no hay dos notas distintas que sean consonantes entre sí. ¿No es eso?
Una cosita, no cuestiono que sabes mucho del tema y tampoco pretendo ser indiscreto, pero me agradaría saber que tienes alguna carrera universitaria u otro tipo de formación musical.
Ojo, no te confundas y valora el orden del magnitud del que hablamos. Ciertamente, la única consonancia exacta es la octava; pero, a efectos prácticos, siguen manteniéndose las demás.
La diferencia entre tu E5 pitagórico y el mío igualmente temperado no llega siquiera a un hercio y la proporción quinta/fundamental de un acorde como La mayor (A4 – C#5 – E5) es de 1,4983. Hablamos de menos de dos milésimas en relación a la consonancia perfecta 1’5.
¿Crees que el oído percibe la diferencia? 😉
Es cierto, la diferencia es prácticamente inaudible, pero yo, en mi condición de científico, no me conformo con que sea «más o menos» lo mismo. Te propongo la siguiente prueba: en un programa de audio (como audacity) genera dos sonidos, uno de 660 Hz y otro de 659,255 Hz. Efectivamente, cuando los reproduces uno seguido de otro no notas ninguna diferencia, pero si los superpones pasa algo muy curioso…
A lo mejor estoy siendo un poco pijotero, pero ya digo, no me entra en la cabeza como la música puede no ser perfectamente exacta.
En efecto, es lo que se conoce como batido. Escuchas una frecuencia entre las dos con una modulación en amplitud de frecuencia la diferencia entre ambas.
Tu duda es absolutamente razonable, eso no es ser pijotero en absoluto. A mí, como físico, también me costó comprenderlo: dada una frecuencia fundamental sus armónicos son múltiplos EXACTOS de ella, y de esta relación de armónicos construimos las notas de nuestra escala.
De modo que, aunque resulte paradójico, la respuesta es que la música es completamente exacta, no aproximada.
El problema surgió (y para eso es bueno que investigues sobre historia de la música) cuando quisimos introducir el concepto de tonalidad y pretendimos seguir manteniendo la misma relación exacta de frecuencias.
Imagina un instrumento afinado en la escala de Do mayor, con sus números exactos, tal como determinan las leyes de la física. Si quieres transportar una pieza a, por ejemplo, Re mayor, ciertas notas (como MI, sin ir más lejos) deberían ser reajustadas ligeramente para mantener la misma proporción en relación a la tónica).
Eso es algo completamente inaceptable desde el punto de vista práctico (imagina tener que reafinar un piano cada vez, o tener un piano para cada tonalidad).
Se eligió, tras muchas idas y venidas, un compromiso pragmático lo suficientemente satisfactorio: la partición logarítmica a espacios iguales. La única exactitud recae en la octava, pero las demás están tan, tan próximas, que en ningún momento se dejan de percibir esas armónicas y matemáticas relaciones fundamentales.
Entonces, ¿crees que se podría construir alguna especie de sintetizador que permitiría reafinarlo en función de la tonalidad en la que se toque con sólo pulsar un botón?
Por supuesto.
Una de las razones por la que me gusta la música electrónica es porque con un ordenador puedo manipular exactamente las frecuencias a mi gusto.
A mí, en particular, más que modificar nuestro sistema igualmente temperado para obtener fracciones de enteros, me interesa la posibilidad de alcanzar microtonos, lo que supone un nuevo universo de expresión musical.
Lo que no me queda claro es qué frecuencias tendrían las diferentes notas en una escala determinada. ¿Guardarían todas las relaciones de números enteros sencillos respecto a la tónica?
Hay toda una gran colección de escalas que se basan en proporciones justas. La más simple conecta con tu duda del comienzo. Simplemente ponte a calcular quintas y reduce el resultado a la primera octava. Obtendrás la escala pitagórica.
Esto parece un círculo vicioso… ¿No volvemos entonces al problema de la quinta del lobo?
Entre otros.
¿Por qué si no habría de inventarse el temperamento igual?
Tres medios elevado a cualquier potencia entera nunca será un múltiplo de 2 porque el numerador es impar y el denominador par.
Tú eliges, ¿te quedas con quintas justas o prefieres octavas justas? Una octava no afinada es muchísimo más cantoso que una quinta que no lo está, de modo que parece sabia la decisión de cuadrar las octavas.
Nunca podremos tener todo, hay que tomar decisiones.
A lo largo de la historia de la música se han ido favoreciendo ciertos intervalos en detrimento de otros, lo que ha originado diferentes tipos de afinaciones.
El camino es apasionante y te recomiendo su estudio, pues parece interesarte el asunto.
No obstante, pese a lo extendido de nuestro desafinado sistema igualmente temperado, hay muchos partidarios de las afinaciones justas (fracciones enteras, música libre de batidos). Para todos estos los cambios de tonalidad no suponen ningún problema, pues entienden que la música debe sonar diferente dependiendo de en qué tonalidad haya sido escrita (como sucedía antes de nuestra afinación actual).
Las transposiciones de tono son un invento consecuencia del temperamento igual.
Tiene sentido cientifica y epistemologicamente,ya que no debio llamarse bien temperado…sino sistema impuro sucio e imperfecto…el cual necesito una metamorfosis,lograda por rene vaderi…para rectificar los errores del temperado.
Amigos,se reconoce su esfuerzo,pero ,temo decirles que …1o. los Savarts,no permiten la cuantificacion por cents….2o. la relacion 3/2,no es 1.4983….3o.el logaritmo desarrollado por pitagoras,fue erroneo….mayor info…facebook : Rene vaderi…cientifico «musical» mexicano.
Javier Montero, mis respetos = ), gracias por la información ! Te felicito !
Un placer, Ariel.
Muchas gracias
Javier, Natanael.. felicitaciones,..Me encantò la discusiòn..!. Sabidurìa pura..!
Javier.. si nos rijieramos por el LA natural 432. (que fuè cambiado por el ministro de cultura aleman en la dècada del 1930 ) esos càlculos, ¿darìan las mismas diferencias..?
y cual fuè el sentido pràctico del cambio del 432 al 440..?
gracias.. hugostinhos@gmail.com
Muchísimas gracias!
Se mantendrían las mismas proporciones, o diferencias logarítmicas (que podrías medir en cents, por ejemplo), pero no las diferencias lineales, que dependerán de qué nota tomes como referencia.
La elección de A 440 fue una larga batalla histórica en la que no sólo competía 432, sino muchas otras, cada una con sus propios argumentos que la justificaban. Simplemente, una tenía que ganar.
Lo de 432 Hz es otro tema apasionante, os recomiendo este vídeo (y, a la vez, todo el canal de Aldo Narejos): https://www.youtube.com/watch?v=Ty9MhvXEH_o.
No conocía esos vídeos. Muy interesantes, desde luego.
Coincido con él. Hay mucha energía desperdiciada tratando estos temas. La elección de una referencia es completamente arbitraria, da igual una que otra, es pero necesaria por respeto a muchos instrumentos cuya reafinación es complicada o incluso imposible.
Excelente explicación. Voy a usar ese ejemplo en mis clases. Me enseñaste algo nuevo, muchas gracias !
Un placer, Helen.
¡Genial, úsalo con total libertad!
Gracias.
muchisimas gracias por esta informacion!!! está muy bien explicado y fue sencillo aprenderlo 😀
Hola! Muchas felicidades por el post, me gustaria que me ayudaras con una duda.
¿Seria posible afinar todas las cuerdas de una guitarra u otros instrumentos con un afinador electrico de 440hz pero 50 centesimas menos en cada nota, para poder «acercarse a una afinacion a 432hz?
Digamos que afinaramos un La, «50cent» menos tendriamos un Sol# «agudo», ¿seria posible que este tono que conseguimos fuera un La 432hz?.
No soy experto en el tema, pero me gustaria afinar mis instrumentos en 432hz con un afinador comun, y pues te agradeceria la ayuda.
Saludos cordiales
Abraham
Qué tal:
Lo más sencillo es utilizar un afinador que te permita modificar la frecuencia del A4 de referencia a valores diferentes de 440 Hz. Hay variedad de modelos muy económicos.
Saludos
La mayoría de afinadores para guitarra, incluso los baratos de pinza, suelen tener un modo «cromático» (además de los normales de guitarra, bajo, ukelele, banjo, etc.) que te permite hacerlo. Aunque antes tendrás que calcular tú mismo la frecuencia de cada cuerda o usar el método de afinación «a oído»; con la guitarra es muy fácil si tienes buen oído porque la quinta cuerda es un La2 (216 Hz) y la relación entre cuerdas es exacta (ya sabes, quinto traste de la sexta es la quinta al aire, etc.); con otros instrumentos no sabría decirte.
Yo uso mucho este método para tocar la guitarra acompañando a flautas dulces, que suelen estar afinadas en La(432); es más fácil (y rápido) reafinar la guitarra (aunque tiene su truco) que andar moviendo la boquilla de la flauta(s) 🙂
hola Javier, gracias por tus explicaciones como músico me has aclarado conceptos básicos que se tendrían que saber, hay una cosa que me llama la atención es el hecho de que entre Mi i Fa y entre Si Y Do se estableciera que tenia que haber semitonos para establecer lo que seria la escala madre para formar las escalas? Luego también comentar te que estoy muy metido en el tema de la afinación en 432 creo que es apasionante investigo con el como terapeuta y puedo decir que la diferencia es muy notable a como respondia la gente cuando trabajaba en 440, creo que es un tema a tomar muy en cuenta, hay videos muy buenos http://www.432hz.com por ej esta muy bien.Gracias por compartir tus conocimientos Ricard
¡Qué tal, Ricard!
Es necesario remontarse en el tiempo y seguir las transformaciones por las que ha ido pasando nuestra concepción musical para poder entender verdaderamente nuestro sistema actual. Es un tema apasionante del que me gustaría ocasionalmente escribir en el blog.
No soy particularmente devoto de la afinación a 432 Hz. Me es difícil imaginar algún tipo de ventaja, no ya en el plano musical, sino en cualquier otro. Pero me interesa muchísimo la opinión de la gente que se toma en serio el asunto, como tú, de modo que prometo ver con atención y sin prejuicios esos vídeos.
Muchas gracias por pasarte y aportar. Seguimos hablando…
De acuerdo con usted Javier…Dudo mucho que que se pueda apreciar la diferencia de ocho hertz,,solo un fenómeno privilegiado de oídos que se podría jactar de captar algo que no tiene ninguna ventaja….Son poquísimos los que pueden percibir la diferencia entre un sostenido y un bemol….A propósito ¿podría hablarnos sobre las 9 comas que existen entre un tono y otro,,cuantos hertz,,cuantas entre los semitonos etc.?….¿Son 12 notas o 17 para los aventajados de oídos?…….Soy un un curioso y admirador de estas asombrosas relaciones, y al leer sus comentarios veo en usted un verdadero profesor….Saludos.
Buenos días, Arturo:
Más que un profesor prefiero definirme como alguien curioso también. Tomo nota de tus peticiones y prometo realizar un nuevo artículo que sirva para debatir sobre todas estas cuestiones.
Gracias por pasarte.
Si gracias Javier, hay un video relmente bueno a mi entender que toca muy bien todo el tema de la música desde sus orígenes sumerios podríamos decir y todo el tema relacionado con la geometría es fascinante. nos vemos….
Gran post y grandes los comentarios. Perfectamente explicados todos y cada uno de los aspectos que se han ido tratando.
rigor + sencillez = genialidad!
Gracias, Javier
Muchas gracias, Jorge. Entonces, seguro que te gustará el artículo que estoy preparando, continuación, en cierto modo, de este. 😉
Saludos
tengo un mini piano en Java, tengo entendido que para que suene la nota de DO es el número 60 y sí da la nota en el código, pero cuales son RE, MI, FA, SOL,LA y SI?
Qué tal, Gerardo:
Ese número 60 no es otro sino la asignación MIDI correspondiente al Do central. Los números de nota MIDI son consecutivos, de modo que la siguiente nota, Do# tiene por código 61, Re el 62, Re# 63, Mi 64, Fa 65 y así sucesivamente.
Saludos
Eres muy amable! Saludos y sería bueno que dieras un twitter o facebook para seguirte.
Saludos
En la columna derecha, arriba, aparecen tanto la cuenta de twitter como la página de Facebook.
Saludos
Buenas.
Solo me pasaba a comentar una cosa.
E error no está en si la secuencia matemática es perfecta o no, el error se encuentra en la distribución de las notas, por lo que el resto ya de por sí se cae solo.
Por muchas matemáticas en las que nos basemos, al final, tenemos que tomar algo como referencia, algo que es infinito, y una vez tomado un punto de referencia, empezamos a crear el resto que ya sabemos, pero… ¿cómo elegir ese punto de referencia perfecto?
Os haré una pregunta respecto al tema del desarrollo de la música a lo largo de la historia, ¿el ser humano era libre en tiempos del medievo o en Grecia, o existían grupos reducidos de poder quienes eran los que decidían que rumbo tomaría la humanidad? ¿nuestros ancestros eran intelectuales o se dedicaban a la ganadería y la agricultura, semi-esclavizados, mientras otros decidían la parte «intelectual»? ¿qué nos hace pensar que la distribución de notas es la correcta o perfecta si una minoría decidió por nosotros? ¿por nuestro bien…? ¿esos mismos que nos utilizaban como herramientas mientras ellos no hacían más que jodernos, nos iban a dar la libertad y la sapiencia? No seamos ignorantes…
Es evidente que en Grecia, todo este conocimiento estaba preservado a unos pocos, de igual forma que es evidente que dicho conocimiento no se obtuvo en esa época, sino que provenía desde tiempos muy remotos, anteriores a la historia oficial.
Hicieron el paripé, para que todo cuadrara de forma «natural» en el camino del desarrollo humano, lo cierto es que esto ya se sabía, pero no tocaba aún ponerlo en evidencia, hasta la época «griega», y que curiosamente estos pequeños grupos de poder, en este caso «filósofos», eran todos sin excepción judíos y cabalistas.
Teniendo esto en cuenta, es evidente que la distribución de las notas no es la correcta, no es la perfecta que es por creación, y por tanto, no es armónica.
Todas las notas han de ser armónicas unas con otras, han de resonar de forma perfecta las unas con las otras, pero en cambio, en el que utilizamos hoy, la única que resuena bien, es evidentemente y obviamente, la octava más aguda o más grave respecto a la nota que estás tocando en ese momento, cosa que es totalmente señal de que algo falla, no cuadra, o como yo lo llamo, nos la han metido doblada.
Por otro lado, el hecho de que distribuyan así las «notas», se hace por varios motivos, el más importante, es por algo que explcaré unas líneas más abajo, y que la frecuencia de resonancia del cofre de la pirámide de Keops, es de 440 Hz, ¿os suena dicha cifra?
¿por qué?
Porque la música se utiliza como fuente energética, para abrir o rasgar el tejido de la cuarta densidad de esta realidad, permitiendo el acceso de ciertos seres (djinns, entre otros nombres) a esta realidad, estableciendo una conexión entre ambos mundos que permite el paso de los ya mencionados, de su realidad a la nuestra, evidentemente hablamos de su ingresión en la cuarta dimensión de esta realidad, por lo que no pueden acceder al plano físico directamente sino a través de métodos «indirectos», a grandes rasgos, el funcionamiento de que todo esto se pueda llevar a cabo es el siguiente:
Tenemos el emisor, el cual es primordial pues es la fuente energética, sin él, el resto sería vacío.
Por tanto, dicho emisor, un ser humano o una multitud de humanos, utilizando como catalizador la música, utilizando la cimática y el funcionamiento de las vibraciones en el cosmos, se consigue el drenar la energía necesaria, para dar el siguiente paso, que se trata de absorber la energía o acumularla en un punto concreto, dicho punto, en la antigüedad, se le llamaba o denominaba de muchas maneras, templos, catedrales, mezquitas, etc, en la actualidad su utilidad ha quedado más o menos reducida, aunque se sigue empleando sea con o sin música, estos «lugares sagrados» debido a su estructura, utilizando ciertas formas geométricas, y evidentemente una cúpula que permite o sirva de escape a la energía acumulada, sirven de capacitadores, para el siguiente paso.
El siguiente paso consiste en enviar la energía necesaria del capacitador, a través de un conducto, a las pirámides, este paso se lleva a cabo utilizando las corrientes telúricas naturales del planeta Tierra, que sirven de puente, por ello no es casual que dichas construcciones, como catedrales, por citar un ejemplo, estén construidas en centros específicos de
segundo orden de dichas corrientes telúricas, las cuales absorben la energía y la conducen siguiendo un patrón que ahora no es momento de explicar ni tiempo.
El siguiente paso es que dichas energías lleguen a las pirámides, una vez allí, las pirámides se encuentran alimentadas y por tanto pueden cumplir su función, que es la de generar vórtices hiper-dimensionales o rasgaduras del tejido tetradimensional de esta realidad a través de las líneas Hartmann permitiendo la entrada o simplemente realizando una abertura por donde alguien puede acceder ( al plano tretradimensional), para esto a muy grandes rasgos se utiliza la música y la afinación de 440 Hz, la de 432 Hz es aún más peligrosa, pues permite y facilita la posesión, pero esto es otro tema.
EN PRINCIPIO AFINAR A UNOS 442 Hz, ssería suficiente.
En cuanto al tema de las notas, en otro moment ocomentaré más al respecto, pero de seguro qeu no son las que han de ser por naturaleza, mi tiempo es limitado.
Saludos.
Interesante perspectiva, gracias por compartirla.
Saludos!
interesante tu explicacion porfavor dame tu facebook o tu correo electronico para ampliar un poco lo que dices . saludosss
Ante todo, enhorabuena por sus magníficas explicaciones. Tengo una duda y le ruego me ayude a esclarecerla. Exactamente por qué se multiplican y no se suman los intervalos?
Muchas gracias
Qué tal, Luis:
Las relaciones geométricas, en vez de aritméticas, que se aprecian entre las frecuencias de las notas musicales obedecen a conclusiones derivadas de fenómemos físicos observables.
Imagina una cuerda tensa de longitud L, sujeta en ambos extremos, produciendo, por ejemplo, una nota de frecuencia de 200 Hz al vibrar. Si esa cuerda la cortas por la mitad (es decir, multiplicas su longitud por 1/2), se observa que la frecuencia resultante es dos veces (la inversa de 1/2) la anterior, 400 Hz. Es la consonancia más perfecta y musicalmente se denomina octava. Observa que, este caso, la distancia entre ambas octavas es de 400 – 200 = 200 Hz. Si la relación fuera lineal podríamos creer erróneamente que la siguiente octava por encima de 400 Hz se encontraría a 400 + 200 = 600 Hz. Pero no es así…
Para obtener el sonido de la nueva octava, volvemos a dividir la cuerda que ya habíamos partido a la mitad, otra vez por la mitad. La frecuencia que se obtiene es de nuevamente el doble: 2 x 400 = 800 Hz. Si comenzamos por 200, la octava siguiente la encontramos a 400 Hz, después a 800 Hz y así sucesivamente. Es decir, hay un factor multiplicativo de 2 entre cada octava.
Ese mismo razonamiento lo podemos hacer para cualquier otro intervalo, no sólo la octava. Si vimos que la mejor consonancia la obteníamos dividiendo la cuerda por la mitad, relación 1/2, la siguiente consonancia mejor a la octava la encontramos con una nueva proporción de enteros, 2/3. Si acortas la cuerta de longitud L dejándola en 2L/3 obtienes lo que en música se denomina quinta justa pura, que es una frecuencia 3/2 (inversa de 2/3) la anterior. Si la cuerda inicial suena a 200 Hz, su quinta justa pura lo hace a 200*3/2 = 300 Hz. La diferencia entre ambas frecuencias es de 300 – 200 = 100 Hz. Para calcular una nueva quinta justa por encima de 300 volvemos a multiplicar por 3/2, obteniendo 450 Hz. La distancia entre ambas quintas es ahora de 450 – 300 = 150 Hz, frente a los 100 Hz que había antes. Conforme vas calculando más quintas, esa distancia se va haciendo mayor, pero el factor multiplicativo entre ellas permanece constante.
Y esto mismo lo puedes hacer extensivo a los restantes intervalos, incluso al más pequeño, el semitono. La frecuencia de un semitono se obtiene siempre multiplicando la del anterior por un factor constante.
Saludos
Una alternativa a cortar una cuerda es tomar una guitarra y elegir una cuerda cualquiera. Por ejemplo, el bordón. Si la pulsamos al aire nos dará la nota Mi. Pues bien, si la pulsamos en el traste número 12, que es justamente la mitad de la longitud de la cuerda (lo podemos comprobar con un metro), nos dará nuevamente Mi en una octava más aguda. La longitud del trozo que suena es la mitad y la frecuencia es el doble, dado que la frecuencia es inversamente proporcional a la longitud.
Si el bordón tiene, al aire, una frecuencia aproximada de 82,4 Hz por segundo, en el traste 12 tendrá 164,8 Hz.
Hola, muy interesante la informacion de esta pagina.
Yo tengo una consulta, hay alguna forma para clasificar intervalos en consonantes y disonantes a partir de la proporcion entre las frecuencias correspondientes a cada nota de dicho intervalo?
Es decir, los ratios 2:1 y 3:2 corresponden a intervalos de octava y quinta, ambos justos,
por ende consonantes. Mientras que si no calcule mal, el ratio de un intervalo de septima mayor es 17:9, lo cual corresponde a un intervalo disonante.
Hay algun parametro presente en dichas proporciones por el cual yo pueda decir que estas corresponden a intervalos consonantes o disonantes?
Qué tal, Esteban:
No hay ninguna relación numérica que defina si un intervalo es consonante o disonante. Es una apreciación subjetiva: tú fijas el límite a partir del cual consideras un intervalo disonante. Es, además, una apreciación que ha evolucionado a lo largo de la historia de la música.
Por otro lado, un mismo intervalo puede sonar más o menos consonante dependiendo del contexto tonal en que se halle inmerso.
Saludos
Si, es verdad, pero yo estaba pensando en los intervalos aislados de un contexto musical, y clasificados segun la teoria clasica (disonancias absolutas, disonancias condicionales, etc).
En esos casos encontre estas definiciones que estoy tratando de comprobar:
«Los intervalos son clasificados como consonantes o disonantes de acuerdo a la complejidad de la relación matemática de la frecuencia sonora de las notas que lo componen».
«En la consonancia un sonido es agradable para nuestro oído cuando dos frecuencias chocan en menor cantidad. En la disonancia un sonido es rechazado por nuestro oído cuando la interferencia (punto de choque entre dos ondas de cierta frecuencia) ocurre constantemente»
El primero si podria verificarse con los ratios, para el segundo argumento supongo que necesitaria las graficas de las funciones de cada frecuencia.
Todas las teorías clásicas están basadas en apreciaciones subjetivas y culturales. Los clasificaciones acústicas, basadas en criterios objetivos, como las que indicas (hay unos cuantos más), nunca podrán dar una respuesta completa a esas apreciaciones. En particular, por mucho que nos gustase encontrar una respuesta en la simple y bella relación de dos números enteros, no la hallaremos de un modo suficientemente satisfactorio.
Tu duda estaba clara desde un principio. Es la misma inquietud que muchos físicos y musicólogos han tratado de resolver. He recurrido al «contexto tonal» simplemente para destacar lo fútiles que son para un músico estas consideraciones.
Saludos
No tenia idea de nada de esto. Es realmente excelente y apasionante unir la musica, las matematicas y la historia.
En efecto. La historia de la música es una novela apasionante, la leas desde el punto de vista científico, cultural o social.
Saludos
Gracias por tomarte el tiempo de explicar este tema y compartirlo. Es de reconocer tu capacidad didáctica, con sencillez y claridad y paso a paso explicas un tema que a primera instancia no parece tan sencillo
Un placer. La relación entre la música, física y matemáticas es un tema apasionante.
Saludos
Si a la nota La = 432 hz. A una octava 864 y entre medio tono seria a 216 sólo nesecito saber cuál sería el valor de todas las notas en frecuencias hz. Cono referencia La 432 hz.
Buenos días:
Para pasar de una nota a la siguiente un semitono más alta, debes multiplicar la frecuencia de la primera por 1’059.
Es decir, partiendo de La = 432 Hz, La# = 432×1’059 = 457.
Y así sucesivamente. Cada salto de semitono debes multiplicar por ese factor.
Saludos
Excelente articulo!
¡Gracias, Olga!
Hola Javier (y compañía).
Tengo entendido que antiguamente existían teclados (de órgano seguramente) en los que en lugar de una tecla negra, entre dos blancas separadas por un tono, había dos. Una para los sostenidos y otra para los bemoles.
La explicación, que alguien me dio hace muchos años, tendría que ver con el tema de los cromas.
Según parece la distancia de un tono se puede dividir en nueve cromas, y si no me equivoco en música hindú se aprecian esas diferencias.
El caso es que lo que ahora llamamos enarmónicos, no lo eran antes. La tecla de sostenido estaba afinada cuatro cromas más alto que su nota previa, y la de bemol a cuatro cromas por debajo de la nota siguiente.
De tal forma que entre las dos teclas negras habría un croma de diferencia.
C# = C + 4c Db = D -4c
D# = D + 4c Eb = E -4c
etc.
Mis conocimientos matemáticos, no dan para más, a pesar de tus buenas explicaciones, pero intuyo que podría tener que ver con esas pequeñas diferencias que comentabais con Natanel (en el 2013).
¿Puedo estar en lo cierto?
Un saludo,
Buenos días, Eduardo:
La historia de la música y, en particular, de los sistemas de afinación, está repleta de ingeniosas fórmulas e inventos, algunos más afortunados que otros, hasta llegar a nuestro sistema occidental actual. El concepto de «coma» (ojo, no «croma») siempre ha acompañado a esta larga y enrevesada aventura, pero eso es otra historia… 😀
Saludos
Gracias por la aclaración del «coma». Es que hablaba de «oido».
Seguramente por eso no encontraba información en la red.
Saludos.
Debo decirles,que todos los calculos que han expuesto en este canal…estan incorrectos….ya que la 8a. no es consonante ,ni es perfecta…la razon 261.626 sobre C central…..es incorrecta,ya que A 440..es un error de calculo en telemetria….la progresion geométrica, no es una proporcion constante,..incorrecto calcular usando 432 x 1.0594623 para obtener razones….Dada una frecuencia fundamental sus armónicos son múltiplos INEXACTOS de ella, y de esta relación de armónicos NO SE CONSTRUYEN las notas de nuestra escala…..NO EXISTEN,las 5as. ni las 8as. justas, tampoco son perfectas, ni consonantes…..432 y 440…son grasos errores de calculo…..EL DUPLO DE VIBRACIONES DE UN SONIDO…NO ES LA 8a…pitagoras fallo en el calculo nodal.
¿Sería posible obtener alguna aclaración sobre la afirmación «Dada una frecuencia fundamental sus armónicos son múltiplos INEXACTOS de ella»?
Gracias.
Y entons mijo, argumentos por favore, u otra perspectiva. Y que el iluminarnos de conocimiento sea una liberacion para comoartinos todos con humildad. Saludos
Respuesta a gonzalo rene vazq….
Gracias por la información que de forma sencilla y clara, me ha hecho comprender el tema.
Me alegro de que te haya sido útil, Pablo. Gracias por pasarte.
Que apasionante tema…Gracias por ilustrarnos y guiarnos Javier….Soy un convencido que Dios puso en nuestras manos estos recursos para nuestro deleite, y no hemos inventado nada , solo hemos ido descubriendo estas relaciones asombrosas , y que nos permiten manifestar este lenguaje espiritual y sublime que es la música…
Me alegro de que te haya gustado el articulo, Arturo.
¡Gracias por pasarte!
Cómo sería entonces la fórmula para calcular la nota en base a la frecuencia? por ejemplo 14350Hz = ?
Simplemente toma logaritmos,
log(f/440) = d * log r
y despeja d.
En el caso propuesto (14350), d es aproximadamente igual a 60, lo que significa que la nota se halla a 60 semitonos del A4. 60 semitonos son 5 octavas, de modo que la nota buscada es precisamente A9.
Saludos
Te felicito! Muy bien explicado!
de verdad es maravilloso que haya personas con la capacidad intelectual de entender y transmitir a los demas informacion tan valiosa y sobre todo apegada a la realidad cientifica hasta ahora aceptada si pretenciones ni abstracciones pseudocientificas que finalmente a nada conducen en la busqueda de la verdad. muy buen espacio para los que gustan de saber y sobre todo de explorar
Ola !! Recién estoy empezando a estudiar lo que es el sonido como se genera y mi profesor me ha dejado un ejercicio pero no vi fórmulas excepto que ando investigando un poco y lo que pude encontrar fue lo siguiente (lo escribo después del ejercicio) pero tengo duda si está bien o mal. Expongo el ejercicio : si un músico interpreta su guitarra en la nota sol(4) cuya frecuencia fundamental es 392Hz calcula sus El valor en hertzios de suave primeros 4 armónicos relativos .
Lo que encontré es que este valor se va multiplicando x 2. Ósea 1 armónico 392×2 =784hz. 2 armónico 392×3= 1.176. Asi sucesivamente pero en si me gustaría saber x qué se multiplica por 2. Es una fórmula o hay un por qué . Gracias. Un saludo
HE LEIDO YA VARIOS ARTICULOS DE ESTE MARAVILLOSO BLOG. HE ESTADO PREGUNTANDOME JAVIER HACE DIAS, POR UNA INQUIETUD QUE ME HA ENTRADO DESPUES DE VIEJO POR LA ELECTRONICA Y LA MUSICA, SI LAS DIFERENTES FIGURAS MUSICALES(notas y silencios) deberian tener UNA duracion EN TIEMPO REAL, MEDIBLE FISICAMENTE, para que se cumplan las leyes de la naturaleza. Se que suena risible la pregunta pero usted es matemático y físico ya sabe que al final de todo termina imponiéndose un orden en todos los fenomenos de la misma. Admiro profundamente su labor en este espacio y ¡¡es ASÍ como se hace PATRIA¡¡
En un principio, fueron los armónicos. Si la primera nota o fundamental tiene una frecuencia de f hercios, los sucesivos armónicos tienen frecuencias de 2f,3f,4f,5f,….etc, hercios.
Esto ya lo observó Pitágoras manejando las longitudes de las cuerdas, que son inversas de las frecuencias. Así, si hacemos música utilizando una nota primera (fundamental) junto con sus notas armónicas, esta música sonaría totalmente «natural» y totalmente «armónica», nunca mejor dicho. Sería algo así como recrear la naturaleza, re-crearla, y por lo tanto nos «recrearíamos» con ella.
Esta música, construída sobre una «familia» de notas, constituída por una nota madre y sus notas armónicas (hijas), es el objetivo que ha perseguido siempre la llamada «música occidental», que además, para finalizar la pieza musical terminaría descansando en la nota madre (Tónica) consiguiendo esa sensación de feliz descanso o «vuelta a casa» que caracteriza a la música tonal.
Ahora bien, si hacemos música con una determinada familia de notas armónicas, no podremos transportar ni modular a otra «familia» armónica sin tener que utilizar las nuevas notas generadas armónicamente por esa nueva familia, que no tienen por qué coincidir con las notas de la primera familia.
Es algo así como las familias humanas, por ejemplo: Una determinada familia tiene lazos de unión entre sus miembros, y estos miembros a su vez, tienen lazos con otros miembros de otras familias. Total, que para hacer música «armónica» partiendo de los miembros de una determinada familia musical (tonalidad) y poder transportar o modular hacia otra familia de notas, necesitaríamos muchas notas, o muchas teclas para un piano o muchos trastes para una guitarra, etc. No podríamos cambiar de tonalidad sin utilizar a otros miembros de otras familias.
Este reto de mantener, por una parte, la música «natural» y «armónica» ; y por otra parte, hacer una música operativa que no necesitase de un excesivo e impracticable número de notas dentro de una octava.
Este reto, decíamos, ha sido una constante a lo largo de la historia de la música occidental, que finalmente en el siglo XVIII, desembocó en la solución, mayoritariamente aceptada, de adoptar la escala actual del temperamento igual. O sea, 12 intervalos de semitono dentro de la octava. Doce notas, de las cuales elegiríamos a 7 de ellas para formar una familia o tonalidad, de tal modo que, si quisiéramos cambiar de familia, solo tendríamos que elegir de entre las 5 restantes de esas 12.
La pregunta del millón, en este momento, es la siguiente: ¿Cuanto nos estaríamos alejando del paraíso de los armónicos al que nunca quisimos renunciar totalmente?
Para responder a esta pregunta, hay que volver a hablar de frecuencias, y veremos que no nos hemos alejado de forma sustancial. De hecho, otras escalas históricas, como la escala pitagórica o la de justa entonación, también se alejaban más o menos igual y además no conseguían un número de notas tan reducido como el de 12.
Y para comparar las frecuencias entre las notas armónicas, y las de otras escalas históricas, incluída la actual, os recomiendo que veais el estudio que publiqué hace algunos años:
https://heptamusica.wordpress.com/2014/11/11/de-la-serie-armonica-a-la-escala-temperada-tablas-comparativas-de-frecuencias/
Muchas gracias. Un saludo.
Que grande! Estoy aprendiendo un montón de música, y esto aclara muchas cosas
Hola si quiero añadir una 3ªmayor y una 5ªJusta superior a una frecuencia de 200Hz, tienen una distancia de 8 semitonos por lo tanto que operación debo hacer multiplicar esta cifra por 1,05944623^8 ?
Gracias un saludo
Con es, a partir de una frecuencia de 200 Hz, obtienes la frecuencia de la quinta justa superior, ni más ni menos.
El resultado es, aproximadamente, 300 (y, más exactamente, 299,6280272). Es fácil con Excel.
Yo he llegado a la cifra citada para la quinta justa (8 semitonos). Si sigues multiplicando hasta llegar a 12 semitonos, el resultado es de unos 400 Hz (más exactamente, 399,9236011).
Para la tercera mayor ascendente, me sale una frecuencia de 251,9681662.
Javier, un sonoro ¡Enhorabuena! Acabo de descubrir tus explicaciones mientras buscaba, a un nivel muy básico, eso de las distancias en frecuencias entre intervalos o notas. Tus explicaciones, aparte de que me superan en cuanto a conocimientos matemáticos, me han resultado …. hasta comprensibles después de un buen rato intentando seguir tus muy claras explicaciones. Debes ser un pedagogo estupendo. Saludos
Hola Tengo una duda, estoy en musica y me dejaron una actividad y no se como calcular las notas musicales, me dieron una partitura de compases para rellenarla y pues no se como se hace, cuanto es 1/16 (Semicorchea) mas 1/8 (Corchea) Gracias de antemano, espero que me puedan ayudAR
Hola. Felicitaciones Javier Montero, por las lecciones de obtención de las frecuencias de las notas musicales. Pero agregaría algo, yo obtuve la constante de otra manera : (18,01÷16,999=1,0595) . Es más exacta qué dividir 18÷17, porque las matemáticas representadas con el sistema actual de análisis no es perfecto. Por eso el sistema digital de notación, incluso de las computadoras, es imperfecto. La raíz cuadrada de 12, solo es una aproximación. Gracias
Estimado Javier…apasionante…el tema..una consulta….tengo un aplicacion de piano virtual en PC .como podria enlazar el sonido de un piano electrico ( fisico ) ,,,capturando las frecuencias de cada tecla y poder guardarlas en una base de datos para poder reproducirlas en mi piano virtual ?…..si me pudieras dar una idea sera genial…gracias por la respuesta
Saludo javier, excelente explicación, muy detalla. Además, le querio pedir q me permita utilizarla (con su respectiva referencia) para mi explicación sobre la amortiguación de los altavoces, desarrollo temas sobre altavoces y cajas acústicas, tu información me queda perfecta para alargar la explicación.
Gracias por tu conocimientos.
Gracias, me alegro de que te sea útil. Puedes usarla, por supuesto.
Saludos.
Cómo se calcularía la frecuencia del Do medio?
Qué gran nota! me aclaró muchas dudas, pero me gustaría consultarte lo siguiente: ¿el timbre está únicamente relacionado a la forma de la onda o la frecuencia y amplitud también la afectan? Saludos desde Perú!
Todo lo expliacdo es correcto y como ingeniero lo entiendo. Lo que no entiendo como ingeniero y NADIE ha sabido explicarme es por qué el oído humano es tan puñetero como para que las teclas negras le «suenen mal» cuando la separación con la inmedita blanca es la misma que entre dos blancas que no tienen negra enmedio.
Hola Jaime, me gustaría intentar aclarar eso que llamas «el puñetero oído humano». Te aconsejo que leas el siguiente enlace: https://heptamusica.wordpress.com/2014/11/11/de-la-serie-armonica-a-la-escala-temperada-tablas-comparativas-de-frecuencias/
En él yo parto de las frecuencias de los armónicos de una nota cualquiera, sin dar ningún nombre a ninguna nota, sólo identificadas éstas por su frecuencia. De este modo, cuando se viene a nombrar las notas, se ve mucho mejor su distribución según el tipo de afinación de que se trate.
Seguro que tu «puñetero oído se adaptaría mejor a las notas de la llamada «justa entonación», que no son las mismas que las del actual «temperamento Igual» o afinación «bien temperada», a pesar de llamarse del mismo modo.
En fin, me alegraría si te he servido de algo. Un saludo.
Gracias por el enlace.
Un poco denso pero ya lo miraré despacio a ver si de verdad a mí, que no soy músico y que no tengo oído musical, me hace entender el fenómeno.
De frecuencias, armónicos y de logaritmos algo sé.
Hola Javier saludos en el 2022. Te quería preguntar lo siguiente: He bajado un tema que no está en la frecuencia de afinación normal a 440hz. ¿Sabes si existe algún software o app que me detecte con precisión la fr de un tema y si es posible modificarlo a 440hz genial. Gracias de antemano.