Objetivo: mostrar algunas técnicas avanzadas de slicing de listas in situ.
Objetivo: mostrar algunas técnicas avanzadas de slicing de listas in situ.
Todo pythonista que se precie debe estar familiarizado con los mecanismos básicos de slicing de secuencias y sus usos idiomáticos más comunes. Si aún no tienes claro qué significan expresiones como secuencia1[2:5] o secuencia2[::-1], puedes encontrar en el blog diversos artículos que te ayudarán a aclarar este concepto.
Dentro de la gama de secuencias de Python se encuentran las magníficas listas, que tienen una interesante propiedad que las diferencia claramente del resto de secuencias: su mutabilidad, la capacidad de ser modificadas in situ.
Si observamos, con mucha paciencia y dedicación, cómo se comportan las listas en su hábitat natural, podremos ser testigos excepcionales de conductas raramente presenciadas por el ser humano: el slicing en el lado izquierdo de una instrucción de asignación, algo que otras secuencias, debido a su inmutabilidad, no pueden exhibir.
Consideremos, por ejemplo, la lista siguiente:
lista = ['a', 'b', 'c', 'd', 'e']
Ya sabemos que la operación de trocear cualquier secuencia crea un nuevo objeto, pero no afecta al objeto original:
>>> lista[2:4] # una rebanada de longitud 2
['c', 'd']
>>> lista
['a', 'b', 'c', 'd', 'e']
>>> lista [::-1] #invirtiendo la lista
['e', 'd', 'c', 'b', 'a']
>>> lista
['a', 'b', 'c', 'd', 'e']
Si lo que queremos es modificar la lista original para que tome como valor el resultado del slicing, simplemente reasignamos la lista para que, a partir de ese momento, referencie al nuevo objeto:
>>> lista = lista[2:4]
>>> lista
['c', 'd']
Este es el procedimiento general para modificar cualquier tipo de secuencia, sea mutable (listas) o inmutable (tuplas y strings). Nótese que en ningún caso hay modificación in situ del objeto inicial, tan sólo referenciamos una dirección de memoria completamente diferente en la que se halla ubicada la rebanada resultante.
Rebanadas en el lado izquierdo
Como hemos dicho, las listas son unas entidades especiales; su valorada mutabilidad permite una operación muy peculiar: trocear en el lado izquierdo de una instrucción de asignación.
Presta mucha atención a lo siguiente
>>> lista = ['a', 'b', 'c', 'd', 'e']
>>> id(lista)
45699960
>>> lista[2:4] = ['C', 'D']
Hemos generado una rebanada de longitud 2 a la cual asignamos otra lista de longitud también 2. Previamente hemos recuperado la dirección de memoria referenciada por lista simplemente a título informativo. ¿Qué crees que habrá sucedido con la lista original?
>>> lista
['a', 'b', 'C', 'D', 'e']
>>> id(lista)
45699960
Hemos modificado la lista original directamente in situ. Observa que se mantiene la misma referencia de memoria.
Guarda bien esta técnica para cuando necesites modificar con una sola operación un bloque contiguo de elementos en una lista.
¿Qué ocurre cuando la longitud de la rebanada difiere de la longitud de la lista que asignamos en el lado derecho? Supongamos que queremos meter tres elementos en un hueco de sólo dos:
>>> lista = ['a', 'b', 'c', 'd', 'e']
>>> lista[2:4] = ['C', 'D', 'E']
>>> lista
['a', 'b', 'C', 'D', 'E', 'e']
La lista acomoda perfectamente en el hueco los tres elementos, sustituyendo los apropiados y empujando los elementos restantes, aumentando el tamaño de la lista, sin sobreescribirlos.
Es fácil entender entonces la situación contraria, cuando la longitud de la lista del lado derecho es inferior a la del troceo:
>>> lista = ['a', 'b', 'c', 'd', 'e']
>>> lista[2:4] = ['C']
>>> lista
['a', 'b', 'C', 'e']
Llevado al extremo, si en el lado derecho ponemos una lista nula, de longitud cero, encontramos una técnica interesante que nos permite eliminar de un plumazo un bloque contiguo de elementos en una lista:
>>> lista[2:4] = []
>>> lista
['a', 'b', 'e']
En todos estos ejemplos, los dos elementos cortados originales han desaparecido. En su lugar aparecen los nuevos, extendiendo o acortando la lista según sea el caso.
Rebanadas de longitud cero
Un paso particularmente interesante resulta cuando provocamos rebanadas de longitud cero en el lado izquierdo. Una rebanada de longitud cero es aquella que devuelve una lista sin elementos. Observa un ejemplo:
>>> lista = ['a', 'b', 'c', 'd', 'e']
>>> lista[2:2]
[]
El slicing anterior retorna todos los elementos entre el índice 2 y, sin incluir, el índice 2 también, es decir, todos los elementos comprendidos entre el índice 2 y el 1. Naturalmente, no se devuelve nada, pues estamos cortando hacia delante y no podemos retroceder. El mismo resultado se obtendría, evidentemente, con lista[2:1] o lista [2:0].
Veamos cómo se comporta en este caso la operación de asignación:
>>> lista = ['a', 'b', 'c', 'd', 'e']
>>> lista[2:2] = ['C']
>>> lista
['a', 'b', 'C', 'c', 'd', 'e']
Como no hay nada que sustituir, el slicing nulo simplemente cumple su función de inserción en el punto indicado por el valor a la izquierda de los dos puntos.
Un error típico conceptual hubiera sido intentar algo como esto:
lista[2:2] = 'C'
La operación de slicing devuelve una lista; por lo tanto, en el lado derecho de la igualdad debe figurar una lista también:
lista[2:2] = ['C']
Naturalmente, obtendríamos el mismo resultado con el método insert:
>>> lista = ['a', 'b', 'c', 'd', 'e']
>>> lista.insert(2, 'C')
>>> lista
['a', 'b', 'C', 'c', 'd', 'e']
Sin embargo, la técnica del slicing permite, a diferencia del método insert, insertar más de un elemento en la misma operación. El objeto list no dispone de ningún método que sea capaz de hacer esto:
>>> lista = ['a', 'b', 'c', 'd', 'e']
>>> lista[2:2] = ['C', 'D', 'E']
>>> lista
['a', 'b', 'C', 'D', 'E', 'c', 'd', 'e']
Podemos situar también el cursor de inserción justo después del último elemento, lo que provocará que la lista se extienda por la derecha. ¿Cómo lo hacemos?
En nuestra lista de ejemplo de 5 elementos, el último tiene por índice 4, ya que el conteo empieza por cero. Para situarnos más allá de él, fuera ya de la lista, elegimos el valor siguiente, 5, que es precisamente la longitud de la lista. Es decir, de forma genérica, el valor que sitúa el cursor más allá de todos los elementos es len(lista).
Para provocar la rebanada nula en ese índice, podemos elegir, como segundo valor del slice, cualquier número entero, sin importar el que sea, pues la lista no existe a partir de ese índice. Todos estos trozos devuelven la rebanada nula a partir del último elemento:
lista[len(lista):0]
lista[len(lista):3]
lista[len(lista):5]
lista[len(lista):100]
También puede, sencillamente, obviarse, pues su omisión hace referencia, cuando recortamos hacia la derecha, al supuesto índice que habría más allá del último real:
lista[len(lista):]
Resulta más fácil ahora entender esta asignación, que agrega un nuevo elemento al final de la lista:
>>> lista = ['a', 'b', 'c', 'd', 'e']
>>> lista[len(lista):] = ['F']
>>> lista
['a', 'b', 'c', 'd', 'e', 'F']
Esto es equivalente a ejecutar el método append:
>>> lista = ['a', 'b', 'c', 'd', 'e']
>>> lista.append('F')
>>> lista
['a', 'b', 'c', 'd', 'e', 'F']
Curiosamente, cualquier valor mayor o igual que len(lista) generaría el mismo resultado:
>>> lista[100:] = ['F']
>>> lista
['a', 'b', 'c', 'd', 'e', 'F']
Podemos extender, por supuesto, la lista con más elementos de una sola vez, no sólo de uno en uno:
>>> lista = ['a', 'b', 'c', 'd', 'e']
>>> lista[len(lista):] = ['F', 'G']
>>> lista
['a', 'b', 'c', 'd', 'e', 'F', 'G']
El método extend realiza exactamente lo mismo:
>>> lista = ['a', 'b', 'c', 'd', 'e']
>>> lista.extend(['F', 'G'])
>>> lista
['a', 'b', 'c', 'd', 'e', 'F', 'G']
Hemos aplicado al slicing de listas en Python su misma medicina y lo hemos dejado bien troceado en conceptos simples, pero poderosos. Utilízalos a discreción y, ante todo, cuida tus dedos…
Javier Montero Gabarró
http://elclubdelautodidacta.es/wp/2015/12/python-troceando-desde-el-lado-izquierdo/
El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)
El Club del Autodidacta
Consulta el índice completo de artículos relacionados con Python.

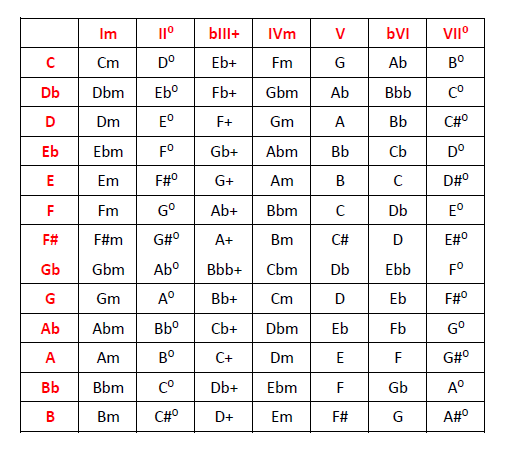
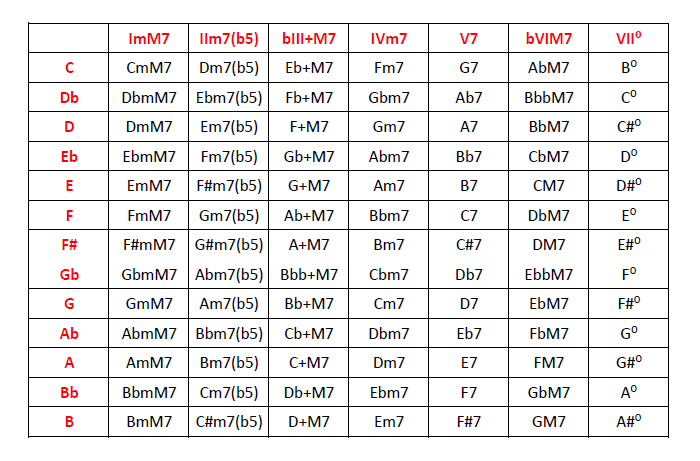
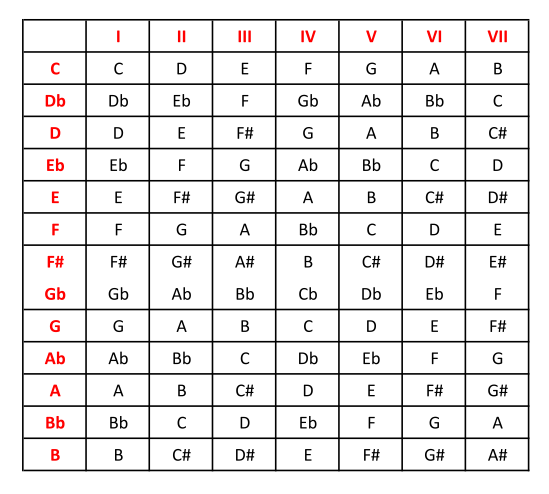
 Objetivo: cuadro de armonización de la escala menor armónica en las 12 tonalidades.
Objetivo: cuadro de armonización de la escala menor armónica en las 12 tonalidades.