Objetivo: cuadro resumen con la escala mayor en las 12 tonalidades.
Objetivo: cuadro resumen con la escala mayor en las 12 tonalidades.
Es esencial para todo músico estar familiarizado con la construcción de escalas, pues constituyen los cimientos sobre los que se asientan las melodías y armonías. Pero, por lo general, no conviene quedarse simplemente con saber razonarlas y construirlas. En la práctica musical es muy conveniente tenerlas en las puntas de los dedos, conocer al momento qué notas y acordes son los que se muestran en cada tonalidad sin tener que interrumpir el flujo creativo para pararse a realizar cuentas matemáticas.
Con el tiempo, el músico acaba familiarizándose con unas tonalidades más que otras. Para lograr un aprendizaje más rápido, consistente y homogéneo hay una actividad que recomiendo encarecidamente: la transposición.
Ejercítate transponiendo a otras tonalidades las armonías y melodías con las que trabajes. Eso no sólo acelerará el proceso de aprendizaje teórico, sino también el mecánico. De este modo evitarás también la dependencia excesiva de mecanismos como la función de transposición de un teclado (que puede ser desastrosa a la hora de sentarte ante un piano real) o de la cejilla para una guitarra.
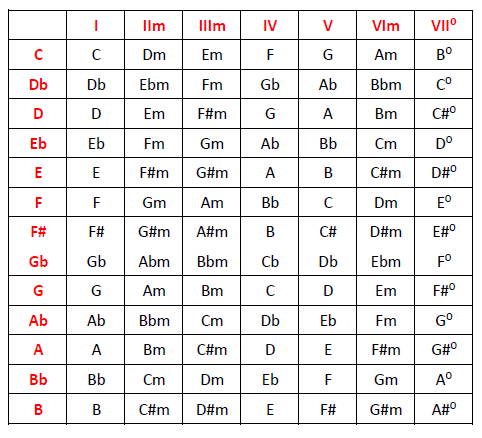
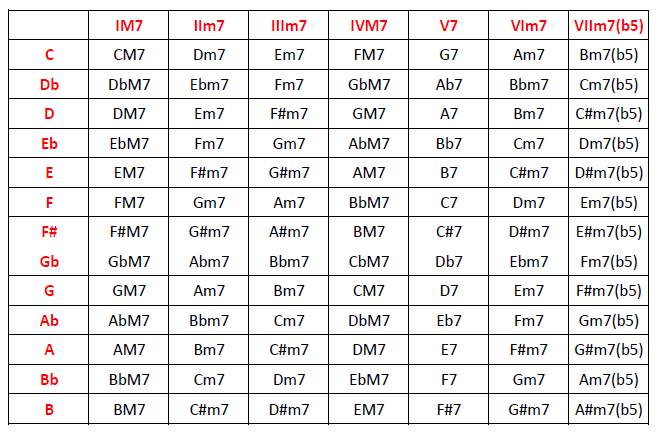
La primera escala a dominar, en sus doce sabores, es la sin duda por excelencia: la escala mayor, que también utilizaremos de referencia para calcular posteriormente otras y para la construcción de acordes. A estas alturas ya debes saber calcularla en cualquier tonalidad, pero lo que vamos a hacer hoy es recopilarlas todas juntas y presentarlas en un cuadro resumen que te conviene tener siempre tener a mano hasta que hayas terminado de interiorizarlas.
Asegúrate de saber deducirla por ti mismo; de lo contrario te será de poca utilidad y el aprendizaje estará cojo.
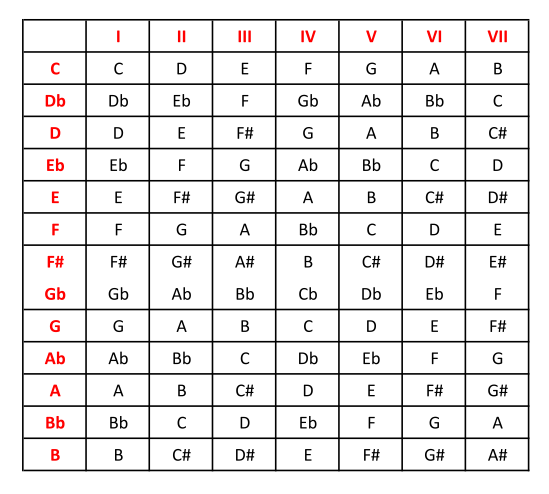
Observa que he elegido los nombres principales ante las opciones enarmónicas (como Re bemol en lugar de Do sostenido), evitando así notas con dobles sostenidos o dobles bemoles. En el caso de F# / Gb, en el centro tritonal, he preferido mantener las dos, no decantándome así ni por béticos ni por sevillistas.
En próximos artículos abundaremos en los usos prácticos de este cuadro, que utilizaremos para el cálculo casi instantáneo de intervalos, escalas y acordes.
Javier Montero Gabarró
http://elclubdelautodidacta.es/wp/2015/09/la-escala-mayor-en-las-12-tonalidades-cuadro/
El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)
El Club del Autodidacta
Índice de todos los artículos de armonía.
Índice de lectura recomendado de la categoría Armonía.