armonización | El Club del Autodidacta

Armonización de la escala menor armónica en las 12 tonalidades

Objetivo: cuadro de armonización de la escala menor armónica en las 12 tonalidades.

En el artículo dedicado a la armonización de la escala menor armónica presentamos los acordes que surgían de modo natural al armonizar, apilando terceras, las notas de esa escala. Recordémoslos en sus versiones de tres y cuatro notas:

Tríadas:

Im – II° – bIII+ – IVm – V – bVI – VII°

El + en el bIII nos indica que se trata de una tríada aumentada.

Tétradas:

Im(maj7) – IIm7(b5) – bIII+(maj7) – IVm7 – V7 – bVImaj7 – VII°

Es importante realizar el pequeño esfuerzo de memorizar estas conclusiones, pero sin descuidar nunca el proceso de saber deducirlas.

Observa que, en estas relaciones, se aprecian los propios grados de la escala menor armónica, además del tipo de acorde. En efecto, si eliminamos este, nos queda:

I – II – bIII – IV – V – bVI – VII

que no es otra cosa sino, precisamente, la fórmula relativa de la escala menor armónica.

Vamos a preparar una tabla recopilatoria con el resultado de armonizar la escala menor armónica en las doce tonalidades comunes, como ya hicimos con las escalas mayor y menor melódica. Constituye, de por sí, una referencia que te podrá ser útil cuando tengas que poner acordes sobre melodías basadas en esta escala; pero es, además, un excelente ejercicio práctico para poner a prueba tus conocimientos de creación de escalas y armonización. Es el tipo de ejercicios que uno debe hacer, al menos, una vez en la vida.

Veamos un ejemplo ilustrativo de la mecánica del problema, por si tienes alguna duda sobre cómo afrontarlo. Imagina que queremos armonizar la escala Re menor armónica.

El primer paso consiste en partir de la escala mayor correspondiente. En este caso, Re mayor.

Re mayor: D – E – F# – G – A – B – C#

A estas alturas esta operación no debería suponerte ningún problema. En caso contrario, consulta, por favor, los artículos referentes a la creación de escalas mayores en cualquier tonalidad.

Una vez establecida Re mayor, deducimos Re menor armónica aplicando su fórmula:

I – II – bIII – IV – V – bVI – VII

Puedes apreciar que debemos bajar un semitono los grados III y VI, dejando intactos los restantes.

Asi pues:

Re menor armónica: D – E – F – G – A – Bb – C#

La nota F# se ha transformado en F natural y el B natural en Bb.

Finalmente, agregamos el tipo de acorde (menor sobre el primer grado, disminuido sobre el segundo, aumentado sobre el tercero, etc.):

Tríadas:

Im – II° – bIII+ – IVm – V – bVI – VII°

Dm – E° – F+ – Gm – A – Bb – C#°

Tétradas:

Im(maj7) – IIm7(b5) – bIII+(maj7) – IVm7 – V7 – bVImaj7 – VII°

Dm(maj7) – Em7(b5) – F+(maj7) – Gm7 – A7 – Bbmaj7 – C#°

La operativa es idéntica para cualquier tonalidad; simplemente, ten la precaución de asegurarte de no repetir dos veces el mismo nombre de nota en la escala, aunque el nombre que te aparezca sea feo o extraño (como Si doble bemol, en lugar de La). Puedes comprobar tus resultados con los de las tablas que figuran a continuación.

Tríadas

Tétradas

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2016/06/armonizacion-de-la-escala-menor-armonica-en-las-12-tonalidades/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice de todos los artículos de armonía.

Índice de lectura recomendado de la categoría Armonía.

Armonización de la escala menor melódica en las 12 tonalidades

Objetivo: cuadro con la armonización de la escala menor melódica en las doce diferentes tonalidades.

Al igual que hicimos hace unos días con la escala mayor, vamos a presentar un cuadro resumen que muestre la armonización de la escala menor melódica en las 12 tonalidades posibles.

Recordemos, en primer lugar, algunos conceptos y conclusiones importantes que en su día trabajamos:

Escala menor melódica: 1 – 2 – b3 – 4 – 5 – 6 – 7

Armonización de la escala menor melódica en tríadas:
Im – IIm – bIII+ – IV – V – VI° – VII°

Armonización de la escala menor melódica en tétradas:
Im(maj7) – IIm7 – bIII+(maj7) – IV7 – V7 – VIm7(b5) – VIIm7(b5)

Recuerda que, a la hora de nombrar los acordes, elegimos el enarmónico que evite la duplicidad de nombres en las fundamentales de cada sucesión. No te sorprenda encontrar, entonces, notas como Fa bemol (en lugar de Mi) o Si doble bemol (en lugar de La).

Dicho esto, he aquí la tabla para acordes de tres notas:

He elegido como referencia de tonalidad mis doce nombres favoritos, que son los que (al menos en las tonalidades mayores), proporcionan nombres de notas más simples y son de uso más común. En el centro tritonal me gusta dejar tanto F# como Gb, pues tanto monta, monta tanto…

Prosigamos con los de cuatro notas:

Para reducir la representación, he optado por la notación alternativa mM7 para el acorde m(maj7) (menor con séptima mayor) y +M7, en lugar de +(maj7) (séptima mayor con quinta aumentada).

Ten a mano estas tablas, como guía de referencia rápida, tanto si trabajas habitual u ocasionalmente con la escala menor melódica o sus modos, pero asegúrate bien de ser capaz de deducirlas por ti mismo.

Javier Montero Gabarró

Armonización de la escala menor melódica en las 12 tonalidades

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Tabla de referencia de construcción de acordes.

Índice de todos los artículos de armonía.

Índice de lectura recomendado de la categoría Armonía.

Armonización de la escala mayor en las 12 tonalidades

Para que sirva de material de referencia cómodo, facilito a continuación unas tablas con los acordes que aparecen al armonizar la escala mayor en cualquier tonalidad, tanto en su versión tríada como tétrada.

Conocer los acordes propios de una tonalidad es algo imprescindible a la hora de componer, arreglar, o simplemente descubrir la armonía subyacente en cualquier canción, pues estos acordes son los que utilizaremos con mayor probabilidad.

La burda memorización es ridícula. Estos acordes sólo terminan de aprenderse mediante su uso repetido al estudiar una tonalidad determinada: no hay mejor forma de conocer los acordes propios de La mayor que tocando piezas en La mayor. Pero eso no excluye tu deber de aprender su deducción. Debes ser capaz de construir estas tablas por ti mismo y en este blog tienes todas las claves para poder hacerlo. Si aún no posees esa habilidad, no lo dejes por más tiempo y ponte manos a la obra cuanto antes, pues son conocimientos imprescindibles para cualquier músico que se tome la armonía en serio.

He simplificado las tablas eligiendo sólo los enarmónicos principales. Esto es, indico la tonalidad de Re bemol, pero no la de Do sostenido, su enarmónico equivalente, pues a efectos prácticos tienen la misma construcción física en el instrumento. El criterio seguido, en estos casos, ha sido optar por la tonalidad de escritura más simple, evitando dobles sostenidos o notas como Si sostenido (enarmónico de Do). En el caso de los enarmónicos Fa sostenido / Sol bemol, he preferido dejar ambas para matizar el hecho de que las dos gozan de la misma importancia «estética» y en ninguna de ellas ha sido posible evitar un nombre de nota feo (E# en la primera y Cb en la segunda).

Estas tablas también pueden ser prácticas para determinar los acordes propios de las tonalidades menores si eres capaz de deducir cuál es la tonalidad relativa mayor correspondiente. No obstante, ten en cuenta que las tonalidades menores son más propensas, por lo general, a la aparición de otros acordes ajenos a la propia escala menor natural. Sin ir más lejos, piensa por ejemplo que existen otras escalas menores de uso habitual, como la armónica y la melódica, y cada una de ellas presenta su propia armonización.

Sin más demora, he aquí las tablas. Comencemos por los acordes de tres notas, las tríadas:

Las tétradas, acordes de cuatro notas:

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2014/11/armonizacion-de-la-escala-mayor-en-las-12-tonalidades/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Tabla de referencia de construcción de acordes.

Índice de todos los artículos de armonía.

Índice de lectura recomendado de la categoría Armonía.

Armonización de la escala menor armónica

Objetivo: presentar los acordes que aparecen tras armonizar la escala menor armónica.

La escala menor armónica debe formar parte del bagaje de todo músico, al igual que, naturalmente, los acordes que surgen en su armonización.

El procedimiento que seguiremos para armonizarla es el mismo que ya hemos repetido en varias ocasiones: partiendo de las notas de la escala, agregaremos sobre cada grado terceras sucesivas y pondremos nombre a los acordes de tres y cuatro notas que nos aparecerán. Si en algún momento te parece que estoy yendo demasiado rápido, consulta, por favor, los artículos anteriores.

Menor armónica: 1 – 2 – b3 – 4 – 5 – b6 – 7

Si no tienes su sonido en la mente, toma tu instrumento y escucha su evocadora y característica melodía. Eso ayudará a crear ambiente y nos introducirá en materia. Percátate de la distancia de tres semitonos entre la b6 y la 7.

Con la fórmula ante nosotros, la escala Do menor armónica resulta obvia:

Do menor armónica: C – D – Eb – F – G – Ab – B

Apilemos terceras tomándolas de la misma escala:

C: C – Eb – G: tercera menor (3 semitonos) + tercera mayor (4 semitonos): tríada menor.

D: D – F – Ab: tercera menor + tercera menor: tríada disminuida.

Eb: Eb – G – B: tercera mayor + tercera mayor: tríada aumentada.

F: F – Ab – C: tercera menor + tercera mayor: tríada menor.

G: G – B – D: tercera mayor + tercera menor: tríada mayor.

Ab: Ab – C – Eb: tercera mayor + tercera menor: tríada mayor.

B: B – D – F: tercera menor + tercera menor: tríada disminuida.

Recopilemos las tríadas que hemos obtenido:

Cm – D° – Eb+ – Fm – G – Ab – B°

Para generalizar a cualquier otra tonalidad distinta de Do menor volvemos a hacer uso de la fórmula relativa, especificando esta vez los acordes deducidos:

Im – II° – bIII+ – IVm – V – bVI – VII°

Apilamos una tercera más y obtenemos las tétradas:

C: C – Eb – G – B
La forma más rápida de identificar estos acordes, conociendo ya la tríada sobre la que se sustentan, consiste en identificar qué tipo de séptima tenemos. Recordemos: la séptima es mayor si está a un semitono de la octava, menor si lo está a dos y disminuida si dista tres semitonos. En nuestro caso, B y C están a un semitono, luego la séptima es mayor. Como la tríada es menor, el acorde resultante es Do menor con séptima mayor, Cm(maj7).

D: D – F – Ab – C
Tríada disminuida con la séptima menor (C y D están a dos semitonos), de modo que estamos ante Dm7(b5) (también se conoce a este tipo de acorde como semidisminuido).

Eb: Eb – G – B – D
Tríada aumentada con séptima mayor: Eb+(maj7)

F: F – Ab – C – Eb
Tríada menor con séptima menor: Fm7

G: G – B – D – F
Tríada mayor con séptima menor: G7

Ab: Ab – C – Eb – G
Tríada mayor con séptima mayor: Abmaj7

B: B – D – F – Ab
Tríada disminuida con séptima disminuida (observa los tres semitonos entre Ab y B): el acorde disminuido completo, B°, también cifrado como Bdim7.

Recopilando:

Cm(maj7) – Dm7(b5) – Eb+(maj7) – Fm7 – G7 – Abmaj7 – B°

Generalizando:

Im(maj7) – IIm7(b5) – bIII+(maj7) – IVm7 – V7 – bVImaj7 – VII°

Demos la bienvenida al acorde disminuido completo en versión tétrada, que es la primera vez que aparece en nuestras armonizaciones.

Te dejo saludándole…

Javier Montero Gabarró

Armonización de la escala menor armónica

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice completo de artículos sobre armonía.

Armonización de la escala menor melódica

Objetivo: deducir los acordes tríadas y tétradas que aparecen al armonizar la escala menor melódica.

Continuando la serie de artículos dedicada a la armonización de escalas menores, vamos a entretenernos hoy construyendo los acordes propios de la escala menor melódica. Como resultado obtendremos acordes nuevos, no presentes al armonizar la menor natural, que enriquecerán nuestras posibilidades a la hora de componer en tonalidades menores.

De modo que coge lápiz y papel; te invito a realizar juntos este sencillo ejercicio.

Partimos de la escala menor melódica, también conocida como menor de jazz por su amplia utilización (juntos a sus modos) en este género.

Menor melódica: 1 – 2 – b3 – 4 – 5 – 6 – 7

Como ves, es parecida a la escala mayor, con la salvedad de que el tercer grado (el que identifica si una escala es mayor o menor) está reducido un semitono, formando una tercera menor con la tónica.

Para nuestro cálculo elegiremos Do menor melódica, extrapolando después las conclusiones obtenidas al resto de las tonalidades.

Do menor melódica: C – D – Eb – F – G – A – B

Al igual que hicimos armonizando otras escalas, apilaremos terceras sucesivas y trataremos de identificar los acordes resultantes.

Calcular terceras es contar de tres en tres incluyendo la primera también. Comencemos por las tríadas:

Tríada sobre C: C – Eb – G
Tríada sobre D: D – F – A
Tríada sobre Eb: Eb – G – B
Tríada sobre F: F – A – C
Tríada sobre G: G – B – D
Tríada sobre A: A – C – Eb
Tríada sobre B: B – D – F

Nombremos los acordes resultantes aplicando lo que sabemos sobre tríadas:

Mayor: Tercera mayor (4 semitonos) + Tercera menor (3 semitonos)
Menor: Tercera menor + Tercera mayor
Disminuida: Tercera menor + Tercera menor
Aumentada: Tercera mayor + Tercera mayor

Por ejemplo, sobre C (C – Eb – G), la distancia entre C y Eb es de 3 seminonos (tercera menor); la distancia entre Eb y G es de 4 semitonos (tercera mayor). De modo que la tríada resultante, una tercera menor más otra mayor, determina un acorde menor, Do menor (Cm).

Repetimos esta operación en los seis restantes acordes, obteniendo:

C – Eb – G: Tercera menor + Tercera mayor: Do menor: Cm
D – F – A: Tercera menor + Tercera mayor: Re menor: Dm
Eb – G – B: Tercera mayor + Tercera mayor: Mib aumentado: Eb+
F – A – C: Tercera mayor + Tercera menor: Fa mayor: F
G – B – D: Tercera mayor + Tercera menor: Sol mayor: G
A – C – Eb: Tercera menor + Tercera menor: La disminuido: A°
B – D – F: Tercera menor + Tercera menor: Si disminuido: B°

Ya tenemos las tríadas buscadas, resultado de armonizar la escala Do menor melódica:

Cm – Dm – Eb+ – F – G – A° – B°

Generalizando sobre cualquier tonalidad, regresando a la fórmula de la escala menor melódica y añadiendo el tipo de acorde obtenido sobre cada grado:

Im – IIm – bIII+ – IV – V – VI° – VII°

Para calcular la versión tétrada, agregamos una tercera más a las que ya teníamos:

Tétrada sobre C: C – Eb – G – B
Tétrada sobre D: D – F – A – C
Tétrada sobre Eb: Eb – G – B – D
Tétrada sobre F: F – A – C – Eb
Tétrada sobre G: G – B – D – F
Tétrada sobre A: A – C – Eb – G
Tétrada sobre B: B – D – F – A

Podemos nombrar las tétradas analizando, como hicimos con las tríadas, el tipo de terceras que las forman, pero el método más rápido de hacerlo pasa por identificar el tipo de séptima. Para ello, contamos los semitonos que la separan de la fundamental del acorde una octava más arriba:

1 semitono: séptima mayor, acorde maj7
2 semitonos: séptima menor, acorde 7
3 semitonos: séptima disminuida, acorde dim7

Por ejemplo, en la tétrada sobre C (C – Eb – G – B), la distancia entre la séptima (B) y la fundamental (C), es de un semitono, de modo que la séptima es mayor. Si a la tríada obtenida (Cm), le agregamos una séptima mayor obtenemos la tétrada Cm(maj7), que se lee como «Do menor séptima mayor».

Procedemos de igual modo con los demás:

C – Eb – G – B: Cm + séptima mayor: Cm(maj7)
D – F – A – C: Dm + séptima menor: Dm7
Eb – G – B – D: Eb+ + séptima mayor: Eb+(maj7) (Mi bemol aumentado séptima mayor)
F – A – C – Eb: F + séptima menor: F7
G – B – D – F: G + séptima menor: G7
A – C – Eb – G: A° + séptima menor: Am7(b5) (también conocido como La semidisminuido, ya que lo está la quinta, pero no la séptima)
B – D – F – A: B° + séptima menor: Bm7(b5)

En resumen:

Cm(maj7) – Dm7 – Eb+(maj7) – F7 – G7 – Am7(b5) – Bm7(b5)

Generalizando, llegamos a esta interesante disposición de acordes, familia propia de la escala menor melódica:

Im(maj7) – IIm7 – bIII+(maj7) – IV7 – V7 – VIm7(b5) – VIIm7(b5)

Próximamente afrontaremos la armonización de otra gran escala menor, la armónica. Pero, ¿por qué esperar hasta entonces? Inténtalo tú mismo; seguro que eres capaz de lograrlo.

Javier Montero Gabarró

Armonización de la escala menor melódica

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice completo de artículos sobre armonía.

Armonización de la escala dórica

Objetivo: presentar los acordes tríadas y tétradas que aparecen al armonizar la escala dórica.

Esta vez iremos rápido. En el artículo anterior de esta serie mostramos con todo lujo de detalles los cálculos necesarios para descubrir los acordes que surgían al armonizar la escala menor natural. Y lo hicimos excediéndonos, aplicando dos caminos diferentes que, como pudimos comprobar, conducían al mismo destino. Por un lado nos aprovechamos del hecho de que la escala menor natural no es sino un modo de la escala mayor (el eólico), por lo que sus acordes propios son exactamente los mismos que los de esta última, sólo que ordenados de modo diferente. Por otro, dedujimos las armonías agregando terceras sucesivas y nombrando los acordes resultantes según el tipo de intervalos que nos encontrábamos.

El caso que nos presenta hoy es semejante: la escala dórica es el segundo modo de la escala mayor.

Es decir, si, por ejemplo, Do mayor es:

Do mayor: C – D – E – F – G – A – B

Re dórica no es otra sino la misma comenzando por Re, el segundo grado:

Re dórica: D – E – F – G – A – B – C

La misma relación de orden sucede entre los acordes de ambas:

Armonización de Do mayor en tríadas:

C – Dm – Em – F – G – Am – B°

Armonización de Re dórica en tríadas:

Dm – Em – F – G – Am – B° – C

Armonización de Do mayor en tétradas:

Cmaj7 – Dm7 – Em7 – Fmaj7 – G7 – Am7 – Bm7(b5)

Armonización de Re dórica en tétradas:

Dm7 – Em7 – Fmaj7 – G7 – Am7 – Bm7(b5) – Cmaj7

Si no comprendes de dónde surgen estos acordes, echa un vistazo a los artículos dedicados a la armonización de la escala mayor.

Para expresar estas relaciones en términos generales, debemos recordar la fórmula de la escala dórica:

Escala dórica: 1 – 2 – b3 – 4 – 5 – 6 – b7

Recuerda que es como la escala menor natural, pero con la sexta mayor (6 en lugar de b6).

Uniendo esta fórmula a los acordes que acabamos de descubrir, obtenemos:

Armonización de la escala dórica en tríadas:

Im – IIm – bIII – IV – Vm – VI° – bVII

Armonización de la escala dórica en tétradas:

Im7 – IIm7 – bIIImaj7 – IV7 – Vm7 – VIm7(b5) – bVIImaj7

No debes obsesionarte por memorizar estas relaciones, pues la escala dórica no se armoniza con frecuencia. Lo importante es que recuerdes los mecanismos para calcularlas cuando las necesites. Si ya tienes en tu memoria los acordes propios de la escala mayor, sólo tendrás que escribirlos y volver a tomarlos desde el segundo para obtener los acordes dóricos sin esfuerzo alguno.

La siguiente escala menor que armonizaremos es la armónica. Estate atento, pues nos visitaran acordes no presentes en la armonización mayor (ni, por lo tanto, en ninguno de sus modos), que enriquecerán nuestras opciones a la hora de componer en tonalidades menores.

Javier Montero Gabarró

Armonización de la escala dórica

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice completo de artículos sobre armonía.

Armonización de la escala menor natural

Objetivo: deducir los acordes que aparecen al armonizar la escala menor natural.

En el artículo de hoy armonizaremos la primera de las escalas menores por excelencia, la menor natural. Es decir, sobre cada grado de la escala apilaremos terceras sucesivas hasta construir acordes de tres y cuatro notas (tríadas y tétradas, respectivamente). Es exactamente lo mismo que hicimos cuando armonizamos la escala mayor.

Deduciremos los acordes de dos formas diferentes. En la primera, casi inmediata, aprovecharemos el hecho de que la escala menor natural no es sino un modo de la escala mayor (el modo eólico). Esto nos ahorrará tener que repetir los cálculos que en su día hicimos con la escala mayor. En la segunda realizaremos el trabajo a mano, agregando cada tercera y poniendo nombre a los acordes resultantes. Todo músico debe estar perfectamente familiarizado con este tipo de cálculos.

Comencemos recordando la formación del modo eólico.

Tomemos como referencia cualquier escala mayor; sin ir más lejos, por su obvia sencillez, DO mayor.

DO mayor: C – D – E – F – G – A – B

El modo eólico se obtiene partiendo del sexto grado utilizando las mismas notas. En nuestro ejemplo, el sexto grado es LA (A). Si construimos, con las mismas notas, la escala que comienza a partir de LA, obtenemos el modo eólico o escala menor natural:

LA eólica (menor natural): A – B – C – D – E – F – G

Conclusión que nos permitía calcular su fórmula relativa:

Eólica (menor natural): 1 – 2 – b3 – 4 – 5 – b6 – b7

De igual modo, si al armonizar DO mayor obteníamos

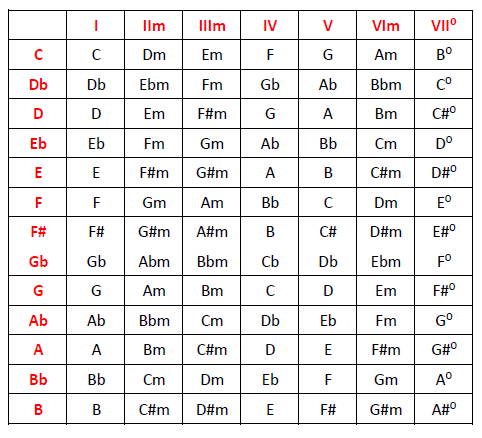
Armonización DO mayor (tríadas):
C – Dm – Em – F – G – Am – B°

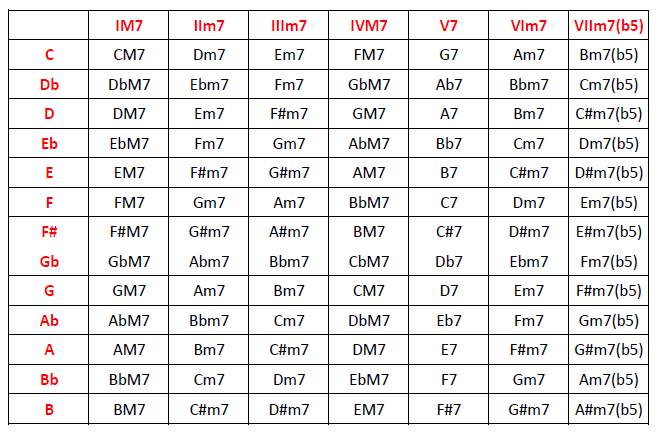
Armonización DO mayor (tétradas):
Cmaj7 – Dm7 – Em7 – Fmaj7 – G7 – Am7 – Bm7(b5)

Comenzando por el sexto acorde (nota fundamental LA) obtendremos la armonización de LA eólica (LA menor natural):

Armonización LA menor natural (tríadas):
Am – B° – C – Dm – Em – F – G

Armonización LA menor natural (tétradas):
Am7 – Bm7(b5) – Cmaj7 – Dm7 – Em7 – Fmaj7 – G7

O bien, en términos generales, basándonos en la fórmula relativa de la escala menor natural:

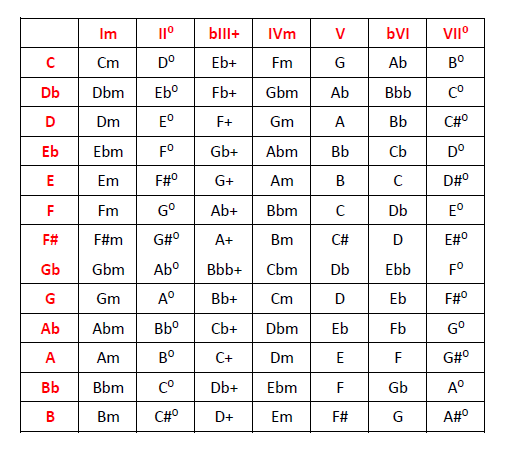
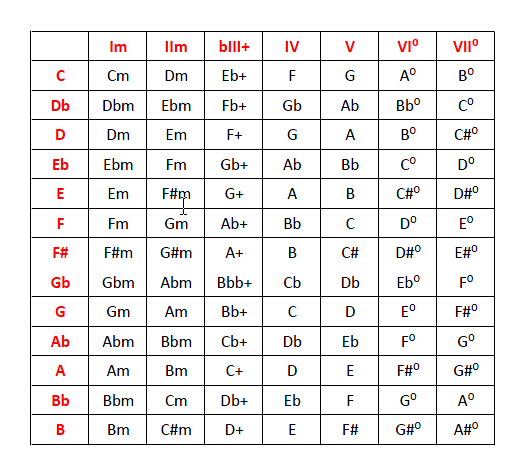
Armonización de la escala menor natural (tríadas):
Im – II° – bIII – IVm – Vm – bVI – bVII

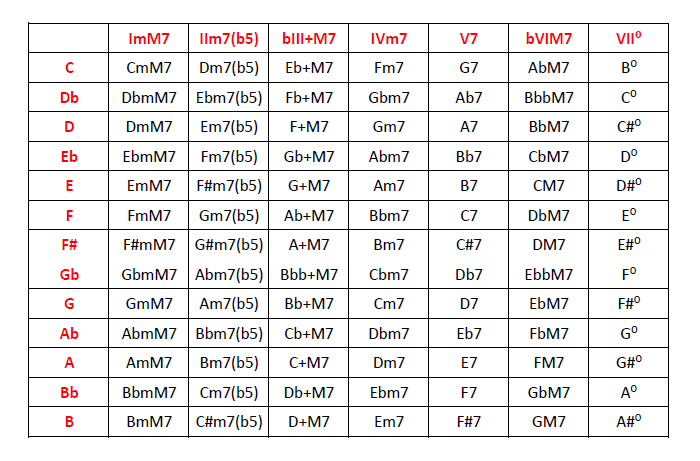
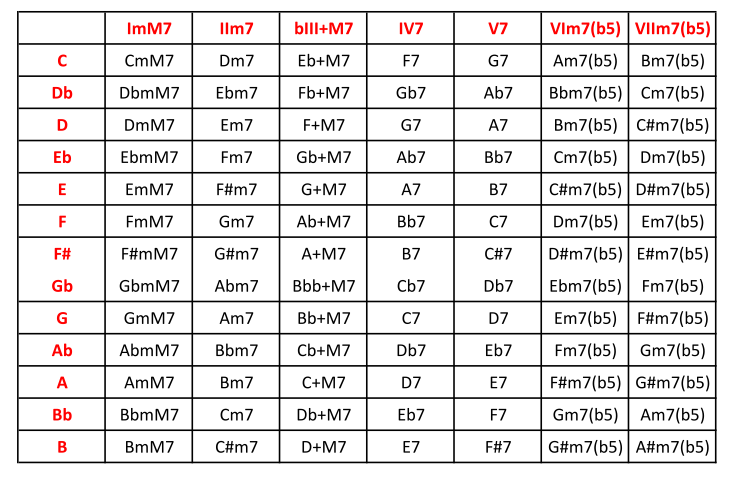
Armonización de la escala menor natural (tétradas):
Im7 – IIm7(b5) – bIIImaj7 – IVm7 – Vm7 – bVImaj7 – bVII7

A lo que quiero llegar con este desarrollo es que observes lo fácil que resulta recuperar estos acordes si los olvidas pero, en cambio, recuerdas los que aparecen al armonizar la escala mayor. Es cuestión de coger exactamente los mismos, pero comenzando en un punto diferente.

Repetiremos esta operación ahora, a modo de ejercicio, por el procedimiento habitual para armonizar escalas heptatónicas que ya empleamos sobre la escala mayor.

Partimos de la fórmula de la escala menor natural y la elaboramos sobre DO:

DO menor natural: C – D – Eb – F – G – Ab – Bb

Construyamos los acordes que aparecen al apilar terceras sobre cada grado.

Contar terceras es contar 1-2-3 sobre las notas de esa escala, incluyendo el punto de origen en la cuenta. Así, por ejemplo, en nuestra escala menor natural, una tercera sobre DO es MI bemol, sobre SOL es SI bemol, y sobre LA bemol es DO.

Empecemos por las tríadas:

Acorde sobre el primer grado: C – Eb – G
Acorde sobre el segundo grado: D – F – Ab
Acorde sobre el tercer grado: Eb – G – Bb
Acorde sobre el cuarto grado: F – Ab – C
Acorde sobre el quinto grado: G – Bb – D
Acorde sobre el sexto grado: Ab – C – Eb
Acorde sobre el séptimo grado: Bb – D – F

Date cuenta que, entre esas terceras, algunas son mayores (4 semitonos de distancia) y otras menores (tres semitonos). En función de cómo estén apiladas el acorde se denominará de un modo u otro.

Recordemos esto:

Tercera mayor + Tercera menor: Tríada mayor
Tercera menor + Tercera mayor: Tríada menor
Tercera menor + Tercera menor: Tríada disminuida
Tercera mayor + Tercera mayor: Tríada aumentada

Sólo hay que calcular intervalos:

C – Eb – G: 3 semitonos + 4 semitonos: Tercera menor + Tercera mayor: DO menor
D – F – Ab: Tercera menor + Tercera menor: RE disminuido
Eb – G – Bb: Tercera mayor + Tercera menor: MI bemol mayor
F – Ab – C: Tercera menor + Tercera mayor: FA menor
G – Bb – D: Tercera menor + Tercera mayor: SOL menor
Ab – C – Eb: Tercera mayor + Tercera menor: LA bemol mayor
Bb – D – F: Tercera mayor + Tercera menor: SI bemol mayor

He aquí, recopiladas, las tríadas resultantes:

Cm – D° – Eb – Fm – Gm – Ab – Bb

En términos generales, sobre cualquier tónica:

Im – II° – bIII – IVm – Vm – bVI – bVII

Resultado que coincide con el deducido más arriba.

También podríamos haber estudiado la composición de cada acorde comparando directamente cada grado obtenido con la fundamental. La primera tercera está a una tercera de la fundamental; la siguiente, a una quinta de esta.

Tercera mayor (4 semitonos) y Quinta justa (7 semitonos): Tríada mayor
Tercera menor (3 semitonos) y Quinta justa: Tríada menor
Tercera mayor y Quinta aumentada (8 semitonos): Tríada aumentada
Tercera menor y Quinta disminuida (6 semitonos): Tríada disminuida

El resultado habría sido el mismo (compruébalo si no has hecho este tipo de cálculos antes). Todas las quintas que aparecen son justas, a excepción de la que sucede sobre el segundo grado, que es disminuida.

Para calcular la versión tétrada de estos acordes apilaremos una tercera más sobre cada tríada obtenida:

Acorde sobre el primer grado: C – Eb – G – Bb
Acorde sobre el segundo grado: D – F – Ab – C
Acorde sobre el tercer grado: Eb – G – Bb – D
Acorde sobre el cuarto grado: F – Ab – C – Eb
Acorde sobre el quinto grado: G – Bb – D – F
Acorde sobre el sexto grado: Ab – C – E – G
Acorde sobre el séptimo grado: Bb – D – F – Ab

La mejor manera de poner nombre a estos acordes pasa por descubrir la naturaleza del último grado añadido. Si te das cuenta, al apilar sobre la fundamental en tríadas hemos obtenido: fundamental + tercera + quinta. El nuevo grado, a una tercera de la quinta, es la séptima del acorde.

Hay que empezar, entonces, averiguando qué tipo de séptima es. Recordemos los tres tipos de séptimas:

Séptima mayor: a 11 semitonos de la fundamental.
Séptima menor: a 10 semitonos de la fundamental
Séptima disminuida: a 9 semitonos de la fundamental

Podemos contar semitonos desde la fundamental de cada acorde. Pero más sencillo es hacerlo al revés, contando la distancia que separa la séptima con la siguiente aparición de la fundamental, la octava. Ambas distancias deben sumar doce.

La tabla anterior puede, entonces, expresarse del siguiente modo:

Séptima mayor: a un semitono de la octava (12 - 11 = 1)
Séptima menor: a dos semitonos de la octava (12 - 10 = 2)
Séptima disminuida: a tres semitonos de la octava (12 - 9 = 3).

Los acordes tétradas se denominan dependiendo de cúal sea la tríada base y la séptima agregada:

Tríada mayor y Séptima mayor: Acorde de séptima mayor: maj7
Tríada mayor y Séptima menor: Acorde de séptima: 7
Tríada menor y Séptima mayor: Acorde menor con séptima mayor: m(maj7)
Tríada menor y Séptima menor: Acorde menor séptima: m7
Tríada disminuida y Séptima menor: Acorde menor séptima b5 o semidisminuido: m7(b5)
Tríada disminuida y Séptima disminuida: Acorde de séptima disminuido: dim7
Tríada aumentada y Séptima mayor: Acorde aumentado con séptima mayor: +maj7
Tríada aumentada y Séptima menor: Acorde aumentado séptima: +7

Apréndete bien esta tabla; te ayudará a comprender de verdad lo que hay detrás de la construcción de acordes.

No todos estos tipos nos aparecerán ahora al armonizar la escala menor natural. Entrarán en escena, a su debido momento, cuando le metamos mano a otras escalas menores como la melódica o la armónica.

Volvamos a nuestras recién creadas tétradas y apliquemos lo expuesto arriba:

C – Eb – G – Bb: Tríada menor y Séptima menor (Bb está a dos semitonos de C): Cm7
D – F – Ab – C: Tríada disminuido y Séptima menor: Dm7(b5)
Eb – G – Bb – D: Tríada mayor y Séptima mayor (D está a un semitono de Eb): Ebmaj7
F – Ab – C – Eb: Tríada menor y Séptima menor: Fm7
G – Bb – D – F: Tríada menor y Séptima menor: Gm7
Ab – C – E – G: Tríada mayor y Séptima mayor: Abmaj7
Bb – D – F – Ab: Tríada mayor y Séptima menor: Bb7

Obteniendo así la armonización de DO menor natural:

Cm7 – Dm7(b5) – Ebmaj7 – Fm7 – Gm7 – Abmaj7 – Bb7

Generalizando a cualquier tónica:

Im7 – IIm7(b5) – bIIImaj7 – IVm7 – Vm7 – bVImaj7 – bVII7

Tal como obtuvimos empleando la primera metodología.

Es importante que te tomes tu tiempo en asimilar y practicar las técnicas que hemos expuesto hoy. Si algo no está del todo claro, asegúrate de que conoces bien otros conceptos como la nomenclatura de intervalos, la formación de escalas y la construcción de acordes. Todos estos temas han sido tratados ya en este blog con anterioridad.

Continuaremos esta serie armonizando otras escalas menores que aún nos quedan en el tintero, pero, ¿por qué no intentarlo tú mismo? Te he mostrado las técnicas y el material de referencia suficiente para poder hacerlo por tu cuenta. Demuéstrate que ya no me necesitas y aventúrate sin miedo. Los fantasmas no son tales cuando se les ilumina.

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2014/01/armonizacion-de-la-escala-menor-natural/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice completo de artículos sobre armonía.

Introducción a la armonización de la escala menor

Objetivo: presentar la serie de artículos que dedicaremos a armonizar los diferentes tipos de escalas menores.

Llegados a este punto, doy por supuesto que ya sabes armonizar la escala mayor en cualquier tonalidad, tanto para generar acordes de tres notas como de cuatro. Si no es así, puedes echar un vistazo al conjunto de siete entradas que hay escritas sobre el tema en este blog.

Es importante que tengas claro el procedimiento que seguimos para deducir los acordes propios de la escala mayor, pues volveremos a aplicarlo ahora, sólo que sobre otras distintas.

Antes que nada, hay una cuestión que conviene matizar. Queremos armonizar la escala menor; pero, ¿cuál es la escala menor? Hay un puñado de escalas menores, ¿a cuál nos referimos?

El enfoque que seguiremos será ante todo práctico. Vamos a partir de las cuatro escalas menores principales (natural, dórica, armónica y melódica), construyendo a continuación, para cada una de ellas, sus acordes propios.

Las cuatro escalas menores indicadas se diferencian en el uso que hacen de los grados sexto y séptimo:

Natural: b6 y b7
Dórica: 6 y b7
Armónica: b6 y 7
Melódica: 6 y 7

A la hora de escribir una canción en tono menor tienes diferentes posibilidades: puedes ceñirte estrictamente a las notas y acordes propios de la escala que te decidas usar o puedes considerar que todas esas notas forman parte de una especie de superescala menor en la que se permite un uso más flexible del b6-6-b7-7 y, a su vez, de los acordes derivados al usar esas notas.

Ambas aproximaciones son perfectamente válidas. A la hora de crear música, debe ser siempre el compositor quien decida qué licencias se toma y los límites que impone a su creación, más que cualquier norma rígida. No lo olvides.

De hecho, hay un grado en particular, disponible en la escala mayor, que se echa mucho de menos al escribir usando las notas estrictas de la escala menor natural: el 7 (en lugar del b7). Y es que, al estar a un semitono de la tónica, invita marcadamente a resolver sobre esta, ayudando a definir con claridad la tonalidad. A este grado se le conoce como sensible y, aunque no está presente ni en las escalas menor natural ni dórica, la armónica y la melódica sí que disponen de él.

Es más, desde el punto de vista armónico, como veremos, la utilización de la sensible permite la aparición del acorde de séptima de dominante sobre el quinto grado de la escala menor, un acorde decisivo para la resolución tonal.

De modo que armonizaremos todas estas escalas menores, agrupando en el mismo saco el conjunto de acordes resultantes, que tendremos a nuestra disposición para poder utilizarlos según nuestros gustos, apetencias y necesidades.

Comenzaremos en el próximo artículo armonizando la escala menor natural. Al igual que sucederá con la dórica, los acordes resultantes serán fáciles de deducir y memorizar, ya que ambas escalas no son sino modos de la escala mayor (la escala menor natural es el modo eólico). Sabemos que los modos comparten las mismas notas, pero comenzando en puntos diferentes. Como consecuencia, de igual forma, los modos comparten también exactamente los mismos acordes y sabiendo los que armonizan la escala mayor sabremos también los que armonizan cualquiera de sus modos.

No será hasta que armonicemos las escalas menor armónica y melódica cuando aparezcan nuevos y suculentos acordes.

Javier Montero Gabarró

Introducción a la armonización de la escala menor

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice completo de artículos sobre armonía.

Armonización de la escala mayor – 7: Ejercicios finales

Objetivo: realización de ejercicios complementarios para asentar los acordes que aparecen al armonizar la escala mayor.

Para concluir esta mini serie dedicada a la armonización de la escala mayor, vamos a dedicar unos minutos a repasar lo aprendido con un par de ejercicios prácticos. Todo lo que necesitas saber para resolverlos es:

– cómo construir escalas mayores en cualquier tonalidad.
– tipo de acordes, por grado, que aparecen al armonizar la escala (tríadas y tétradas).

Ejercicio 1: indicar los acordes tríadas y tétradas propios de la tonalidad Mi mayor.

Comenzamos construyendo la escala Mi mayor, cuyos grados serán las fundamentales de los acordes que buscamos:

Mi mayor: E – F# – G# – A – B – C# – D#

Acordes tríadas: I – IIm – IIIm – IV – V – VIm – VIIº

De modo que nuestras tríadas son:

E – F#m – G#m – A – B – C#m – D#º

Acordes tétradas: Imaj7 – IIm7 – IIIm7 – IVmaj7 – V7 – VIm7 – VIIm7(b5)

En particular, en Mi mayor:

Emaj7 – F#m7 – G#m7 – Amaj7 – B7 – C#m7 – D#m7(b5)

Ejercicio 2: acordes diatónicos de Sol mayor.

Sol mayor: G – A – B – C – D – E – F#

Utilizando las relaciones anteriores:

Tríadas: G – Am – Bm – C – D – Em – F#º

Tétradas: Gmaj7 – Am7 – Bm7 – Cmaj7 – D7 – Em7 – F#m7(b5)

Otro ejercicio que puedes realizar es continuar la extensión de las armonías una tercera más, alcanzando la novena. Si has comprendido bien lo explicado a lo largo de estos artículos, no deberá suponerte mucho problema su realización.

Con tiempo y práctica irás reteniendo los acordes propios de cada tonalidad sin necesidad de realizar los cálculos. Es cuestión de experiencia tonal: si tocas canciones en Fa mayor, por ejemplo, te darás cuenta de que siempre aparecen los mismos acordes y serás capaz de detectar al instante la eventual presencia de cualquier intruso (colocar hábilmente intrusos entre acordes diatónicos es un arte armónico que todo compositor debe dominar y del que hablaremos en ocasiones en el blog presentando métodos comúnmente aceptados de hacerlo).

Cerramos ya la armonización de la escala mayor, pero volveremos más adelante con otras escalas a las que aplicaremos los mismos criterios de construcción de acordes. Como veremos, la armonización de cualquier modo de la escala mayor será una labor obvia, pero tendremos el placer de descubrir nuevos acordes cuando tratemos con escalas menores como la armónica o la melódica.

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2013/06/armonizacion-de-la-escala-mayor-7-ejercicios-finales/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice de todos los artículos de armonía.

Armonización de la escala mayor – 6: las tétradas

Objetivo: Deducir los acordes tétradas que aparecen al armonizar por terceras la escala mayor.

En los artículos anteriores aprendimos a armonizar la escala mayor superponiendo intervalos de terceras y dedujimos los acordes de tres notas (tríadas) que nos aparecían. Obtuvimos el siguiente paquete de acordes:

I – IIm – IIIm – IV – V – VIm – VIIº

en el que los números romanos hacen mención al grado de la escala correspondiente.

Hoy vamos a agregar otra tercera diatónica (es decir, perteneciente a la misma escala) para obtener acordes de cuatro notas, conocidos como tétradas o cuatríadas. Eso nos permitirá ampliar nuestro repertorio tonal con siete acordes nuevos de colorido diferente a su versión en tres notas.

Utilizaremos para el cálculo la escala de Do mayor, generalizando después para el resto de las tonalidades mayores.

Do mayor: C – D – E – F – G – A – B – C

1) Acorde sobre el primer grado:

Partimos de la nota Do (C) y solapamos tres terceras.

C – E – G – B

Observa que un intervalo de tercera es equivalente a saltarse una nota y coger la siguiente.

Al igual que hicimos con las tríadas, descubramos la naturaleza de cada sucesiva tercera, es decir, indiquemos si es mayor (4 semitonos) o menor (3 semitonos).

De C a E: cuatro semitonos; tercera mayor.

De E a G: tres semitonos; tercera menor.

De G a B: cuatro semitonos; tercera mayor.

Tercera mayor + Tercera menor + Tercera mayor = acorde de séptima mayor (maj7 o 7M).

En nuestro caso, partiendo de C, el acorde es Do séptima mayor, Cmaj7.

Para entender mejor la aparición de esta séptima voy a ofrecerte un cálculo alternativo con el que conviene que estés familiarizado. En lugar de calcular el intervalo existente entre una nota y la anterior, vamos a hacerlo en relación a la primera nota del acorde, la fundamental.

Entre C y E, una tercera mayor, como ya hemos visto.

Entre C y G hay una quinta. Si cuentas los semitonos de diferencia obtienes siete, de modo que se trata de una quinta justa o perfecta.

[Si no tienes soltura calculando intervalos, puedo sugerirte la lectura de los ocho artículos de la serie Intervalos sin secretos, en el que se explica toda la teoría junto a numerosos ejemplos prácticos.]

Entre C y B hay una séptima. Se compone de 11 semitonos, de modo que es una séptima mayor.

Todos los intervalos nos han salido mayores, de modo que la fórmula de este acorde es:

1 – 3 – 5 – 7: acorde de séptima mayor, Cmaj7 en nuestro caso.

2) Acorde sobre el segundo grado:

Partimos de Re (D) y apilamos terceras:

D – F – A – C

Realizando las mismas cuentas que hicimos antes obtenemos la siguiente composición intervalica:

Tercera menor + Tercera mayor + Tercera menor = Acorde menor séptima (m7).

O bien, en relación a la fundamental:

1 – b3 – 5 – b7

En nuestro caso, sobre Re, Dm7.

3) Acorde sobre el tercer grado:

E – G – B – D

Tercera menor + Tercera mayor + Tercera menor : Acorde menor séptima (m7), como antes.

1 – b3 – 5 – b7

Con fundamental en Mi, Em7.

4) Acorde sobre el cuarto grado:

F – A – C – E

Tercera mayor + Tercera menor + Tercera mayor = acorde de séptima mayor (maj7 o 7M), el mismo tipo que sobre el primer grado.

1 – 3 – 5 – 7

Con fundamental en Fa, Fmaj7.

5) Acorde sobre el quinto grado:

G – B – D – F

Tercera mayor + Tercera menor + Tercera menor = acorde de séptima (7).

Calculando los intervalos en relación a la fundamental:

1 – 3 – 5 – b7

Observa que la séptima, a diferencia de lo que sucedía sobre el primer o cuarto grado, es menor. Ten presente que, a la hora de formar acordes, si no se especifica de qué tipo es la séptima, se está sobreentiendo que es menor. Sobre el primer y cuarto grados especificamos que la séptima es mayor, de ahí el nombre de los acordes: Do séptima mayor y Fa séptima mayor. Pero sobre el quinto grado la séptima es menor, y por eso decimos sólo Sol séptima, sin más calificativos.

Sobre Sol, pues, G7.

6) Acorde sobre el sexto grado:

A – C – E – G

Tercera menor + Tercera mayor + Tercera menor : Acorde menor séptima (m7), del mismo tipo que sobre los grados 2 y 3.

1 – b3 – 5 – b7

Sobre La, Am7.

En relación al comentario anterior, observa que no especificamos más que séptima, sin el adjetivo menor (el menor que precede al siete hace referencia a que la tercera es menor, propia de los acordes menores, y no califica la séptima, pues por defecto ya lo es). Existe un acorde menor semejante, pero con la séptima mayor, en lugar de menor, Am maj7 y se denomina La menor con séptima mayor. Lo veremos aparecer cuando armonicemos otro tipo de escalas.

7) Acorde sobre el séptimo grado:

B – D – F – A

Tercera menor + Tercera menor + Tercera mayor = Acorde menor séptima con quinta disminuida, conocido también como semidisminuido: m7(b5).

A veces, podrás encontrarte este acorde escrito de un modo diferente: el mismo circulito que empleábamos para los disminuidos, pero con una línea partiéndolo por la mitad: ∅

En relación a la fundamental,

1 – b3 – b5 – b7

Sobre Si, Bm7(b5).

Ya tenemos nuestros siete acordes buscados. Agrupémoslos:

Cmaj7 – Dm7 – Em7 – Fmaj7 – G7 – Am7 – Bm7(b5)

Generalizar al resto de tonalidades mayores es inmediato:

Imaj7 – IIm7 – IIIm7 – IVmaj7 – V7 – VIm7 – VIIm7(b5)

Conclusión: acordes de séptima mayor sobre los grados 1 y 4, menores séptima, sobre el 2, 3 y 6, séptima sobre el 5 (grado conocido como dominante, de ahí la forma común de referirse al acorde de séptima como acorde de séptima de dominante) y menor séptima con quinta bemol sobre el 7.

Al igual que con las tríadas, apréndete bien estos acordes, ingredientes con los que todo compositor prepara sus recetas mágicas.

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2013/05/armonizacion-de-la-escala-mayor-6-las-tetradas/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice de todos los artículos de armonía.

Etiqueta: armonización

Armonización de la escala menor armónica en las 12 tonalidades

Armonización de la escala menor melódica en las 12 tonalidades

Armonización de la escala mayor en las 12 tonalidades

Armonización de la escala menor armónica

Armonización de la escala menor melódica

Armonización de la escala dórica

Armonización de la escala menor natural

Introducción a la armonización de la escala menor

Armonización de la escala mayor – 7: Ejercicios finales

Armonización de la escala mayor – 6: las tétradas

Uso de cookies

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Uso de cookies