escala mayor | El Club del Autodidacta

La escala mayor en las 12 tonalidades – Cuadro

Objetivo: cuadro resumen con la escala mayor en las 12 tonalidades.

Es esencial para todo músico estar familiarizado con la construcción de escalas, pues constituyen los cimientos sobre los que se asientan las melodías y armonías. Pero, por lo general, no conviene quedarse simplemente con saber razonarlas y construirlas. En la práctica musical es muy conveniente tenerlas en las puntas de los dedos, conocer al momento qué notas y acordes son los que se muestran en cada tonalidad sin tener que interrumpir el flujo creativo para pararse a realizar cuentas matemáticas.

Con el tiempo, el músico acaba familiarizándose con unas tonalidades más que otras. Para lograr un aprendizaje más rápido, consistente y homogéneo hay una actividad que recomiendo encarecidamente: la transposición.

Ejercítate transponiendo a otras tonalidades las armonías y melodías con las que trabajes. Eso no sólo acelerará el proceso de aprendizaje teórico, sino también el mecánico. De este modo evitarás también la dependencia excesiva de mecanismos como la función de transposición de un teclado (que puede ser desastrosa a la hora de sentarte ante un piano real) o de la cejilla para una guitarra.

La primera escala a dominar, en sus doce sabores, es la sin duda por excelencia: la escala mayor, que también utilizaremos de referencia para calcular posteriormente otras y para la construcción de acordes. A estas alturas ya debes saber calcularla en cualquier tonalidad, pero lo que vamos a hacer hoy es recopilarlas todas juntas y presentarlas en un cuadro resumen que te conviene tener siempre tener a mano hasta que hayas terminado de interiorizarlas.

Asegúrate de saber deducirla por ti mismo; de lo contrario te será de poca utilidad y el aprendizaje estará cojo.

Observa que he elegido los nombres principales ante las opciones enarmónicas (como Re bemol en lugar de Do sostenido), evitando así notas con dobles sostenidos o dobles bemoles. En el caso de F# / Gb, en el centro tritonal, he preferido mantener las dos, no decantándome así ni por béticos ni por sevillistas.

En próximos artículos abundaremos en los usos prácticos de este cuadro, que utilizaremos para el cálculo casi instantáneo de intervalos, escalas y acordes.

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2015/09/la-escala-mayor-en-las-12-tonalidades-cuadro/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice de todos los artículos de armonía.

Índice de lectura recomendado de la categoría Armonía.

Armonización de la escala mayor en las 12 tonalidades

Para que sirva de material de referencia cómodo, facilito a continuación unas tablas con los acordes que aparecen al armonizar la escala mayor en cualquier tonalidad, tanto en su versión tríada como tétrada.

Conocer los acordes propios de una tonalidad es algo imprescindible a la hora de componer, arreglar, o simplemente descubrir la armonía subyacente en cualquier canción, pues estos acordes son los que utilizaremos con mayor probabilidad.

La burda memorización es ridícula. Estos acordes sólo terminan de aprenderse mediante su uso repetido al estudiar una tonalidad determinada: no hay mejor forma de conocer los acordes propios de La mayor que tocando piezas en La mayor. Pero eso no excluye tu deber de aprender su deducción. Debes ser capaz de construir estas tablas por ti mismo y en este blog tienes todas las claves para poder hacerlo. Si aún no posees esa habilidad, no lo dejes por más tiempo y ponte manos a la obra cuanto antes, pues son conocimientos imprescindibles para cualquier músico que se tome la armonía en serio.

He simplificado las tablas eligiendo sólo los enarmónicos principales. Esto es, indico la tonalidad de Re bemol, pero no la de Do sostenido, su enarmónico equivalente, pues a efectos prácticos tienen la misma construcción física en el instrumento. El criterio seguido, en estos casos, ha sido optar por la tonalidad de escritura más simple, evitando dobles sostenidos o notas como Si sostenido (enarmónico de Do). En el caso de los enarmónicos Fa sostenido / Sol bemol, he preferido dejar ambas para matizar el hecho de que las dos gozan de la misma importancia «estética» y en ninguna de ellas ha sido posible evitar un nombre de nota feo (E# en la primera y Cb en la segunda).

Estas tablas también pueden ser prácticas para determinar los acordes propios de las tonalidades menores si eres capaz de deducir cuál es la tonalidad relativa mayor correspondiente. No obstante, ten en cuenta que las tonalidades menores son más propensas, por lo general, a la aparición de otros acordes ajenos a la propia escala menor natural. Sin ir más lejos, piensa por ejemplo que existen otras escalas menores de uso habitual, como la armónica y la melódica, y cada una de ellas presenta su propia armonización.

Sin más demora, he aquí las tablas. Comencemos por los acordes de tres notas, las tríadas:

Las tétradas, acordes de cuatro notas:

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2014/11/armonizacion-de-la-escala-mayor-en-las-12-tonalidades/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Tabla de referencia de construcción de acordes.

Índice de todos los artículos de armonía.

Índice de lectura recomendado de la categoría Armonía.

La fórmula relativa de los modos de la escala mayor

Objetivo: deducir y recopilar la fórmula relativa de los modos de la escala mayor.

En el artículo de hoy, partiendo de las fórmulas absolutas de los modos de la escala mayor, que ya dedujimos, estableceremos sus fórmulas relativas, esto es, aquellas que relacionan cada grado de la escala con los respectivos de la escala mayor.

El procedimiento ya lo hemos ilustrado anteriormente: utilizando la composición absoluta, calcularemos la escala partiendo de la nota Do, lo que nos permitirá comparar a simple vista las notas obtenidas con Do mayor (aprovechando el hecho de que Do mayor no contiene notas alteradas).

Manos a la obra; empecemos por el segundo modo, el dórico (el primero, o modo jónico, es la propia escala mayor).

Dórica: T – S – T – T – T – S – T

Calculemos las notas de la escala Do dórica:

Si a la nota DO le agregamos un tono, obtenemos RE.

RE más un semitono nos lleva a MI bemol.

Un tono por encima de MIb nos conduce a FA.

Si a FA lo subimos un tono obtenemos SOL.

SOL más un tono desemboca en LA.

Si subimos un semitono LA alcanzamos SI bemol.

SIb más un tono nos devuelve a DO. Esta última operación es siempre de comprobación; si no hubiéramos obtenido DO sería señal de que nos habríamos equivocado en el camino.

Pongamos todas juntas las notas obtenidas:

Do dórica: C – D – Eb – F – G – A – Bb

y comparémosla con Do mayor:

Do mayor: C – D – E – F – G – A – B

Todo coincidencias a excepción del tercer grado y el séptimo, ambos a un semitono por debajo, en la dórica, respecto a los mismos grados de la escala mayor.

Si la escala mayor tiene por fórmula:

Mayor: 1 – 2 – 3 – 4 – 5 – 6 – 7

La comparación anterior nos lleva a la siguiente fórmula para la escala dórica:

Dórica: 1 – 2 – b3 – 4 – 5 – 6 – b7

El siguiente modo, el frigio, se caracteriza por la siguiente composición absoluta:

Frigia: S – T – T – T – S – T – T

Calculemos, entonces, Do frigia:

DO + S = REb
REb + T = MIb
MIb + T = FA
FA + T = SOL
SOL + S = LAb
LAb + T = SIb
SIb + T = DO

Do frigia: C – Db – Eb – F – G – Ab – Bb

Frigia: 1 – b2 – b3 – 4 – 5 – b6 – b7

Como ves, esto no tiene ningún misterio; es una cuestión, simplemente, de no equivocarse en los cálculos.

Voy a seguir con el resto, aunque sería interesante que tú mismo hicieras las operaciones y comprobaras tu resultados con los míos.

Cuarto modo, la escala lidia:

Lidia: T – T – T – S – T – T – S

DO + T = RE
RE + T = MI
MI + T = FA#
FA# + S = SOL
SOL + T = LA
LA + T = SI
SI + S = DO

Do lidia: C – D – E – F# – G – A – B

Lidia: 1 – 2 – 3 – #4 – 5 – 6 – 7

Quinto modo, la escala mixolidia:

Mixolidia: T – T – S – T – T – S – T

DO + T = RE
RE + T = MI
MI + S = FA
FA + T = SOL
SOL + T = LA
LA + S = SIb
SIb + T = DO

Do mixolidia: C – D – E – F – G – A – Bb

Mixolidia: 1 – 2 – 3 – 4 – 5 – 6 – b7

Sexto modo, la escala eólica o menor natural:

Eólica: T – S – T – T – S – T – T

DO + T = RE
RE + S = MIb
MIb + T = FA
FA + T = SOL
SOL + S = LAb
LAb + T = SIb
SIb + T = DO

Do eólica: C – D – Eb – F – G – Ab – Bb

Eólica: 1 – 2 – b3 – 4 – 5 – b6 – b7

Finalmente, el modo locrio:

Locria: S – T – T – S – T – T – T

DO + S = REb
REb + T = MIb
MIb + T = FA
FA + S = SOLb
SOLb + T = LAb
LAb + T = SIb
SIb + T = DO

Do locria: C – Db – Eb – F – Gb – Ab – Bb

Locria: 1 – b2 – b3 – 4 – b5 – b6 – b7

A modo de síntesis, recopilemos estas fórmulas en una tabla:

Jónica ( o mayor): 1 - 2 - 3 - 4 - 5 - 6 - 7

Dórica: 1 - 2 - b3 - 4 - 5 - 6 - b7

Frigia: 1 - b2 - b3 - 4 - 5 - b6 - b7

Lidia: 1 - 2 - 3 - #4 - 5 - 6 - 7

Mixolidia: 1 - 2 - 3 - 4 - 5 - 6 - b7

Eólica ( o menor natural): 1 - 2 - b3 - 4 - 5 - b6 - b7

Locria: 1 - b2 - b3 - 4 - b5 - b6 - b7

Memoriza estas relaciones cuanto antes; no te llevará demasiado esfuerzo.

He aquí unas cantinelas típicas que te ayudarán a hacerlo:

– La escala dórica es como la menor natural (el modo eólico), pero con el sexto grado un semitono más alto (6 en lugar de b6).

– La escala frigia es como la menor natural, pero además tiene el b2.

– La escala lidia es como la mayor, pero con el cuarto grado aumentado un semitono (#4 en lugar de 4).

– La escala mixolidia es como la mayor, pero con el séptimo grado disminuido un semitono (b7 en lugar de 7).

– La escala eólica es la menor natural.

– La escala locria tiene todos los grados reducidos un semitono a excepción del cuarto (y la tónica, naturalmente).

Y nada más por hoy. Be modal!

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2013/12/la-formula-relativa-de-los-modos-de-la-escala-mayor/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice completo de artículos sobre armonía.

Armonización de la escala mayor – 7: Ejercicios finales

Objetivo: realización de ejercicios complementarios para asentar los acordes que aparecen al armonizar la escala mayor.

Para concluir esta mini serie dedicada a la armonización de la escala mayor, vamos a dedicar unos minutos a repasar lo aprendido con un par de ejercicios prácticos. Todo lo que necesitas saber para resolverlos es:

– cómo construir escalas mayores en cualquier tonalidad.
– tipo de acordes, por grado, que aparecen al armonizar la escala (tríadas y tétradas).

Ejercicio 1: indicar los acordes tríadas y tétradas propios de la tonalidad Mi mayor.

Comenzamos construyendo la escala Mi mayor, cuyos grados serán las fundamentales de los acordes que buscamos:

Mi mayor: E – F# – G# – A – B – C# – D#

Acordes tríadas: I – IIm – IIIm – IV – V – VIm – VIIº

De modo que nuestras tríadas son:

E – F#m – G#m – A – B – C#m – D#º

Acordes tétradas: Imaj7 – IIm7 – IIIm7 – IVmaj7 – V7 – VIm7 – VIIm7(b5)

En particular, en Mi mayor:

Emaj7 – F#m7 – G#m7 – Amaj7 – B7 – C#m7 – D#m7(b5)

Ejercicio 2: acordes diatónicos de Sol mayor.

Sol mayor: G – A – B – C – D – E – F#

Utilizando las relaciones anteriores:

Tríadas: G – Am – Bm – C – D – Em – F#º

Tétradas: Gmaj7 – Am7 – Bm7 – Cmaj7 – D7 – Em7 – F#m7(b5)

Otro ejercicio que puedes realizar es continuar la extensión de las armonías una tercera más, alcanzando la novena. Si has comprendido bien lo explicado a lo largo de estos artículos, no deberá suponerte mucho problema su realización.

Con tiempo y práctica irás reteniendo los acordes propios de cada tonalidad sin necesidad de realizar los cálculos. Es cuestión de experiencia tonal: si tocas canciones en Fa mayor, por ejemplo, te darás cuenta de que siempre aparecen los mismos acordes y serás capaz de detectar al instante la eventual presencia de cualquier intruso (colocar hábilmente intrusos entre acordes diatónicos es un arte armónico que todo compositor debe dominar y del que hablaremos en ocasiones en el blog presentando métodos comúnmente aceptados de hacerlo).

Cerramos ya la armonización de la escala mayor, pero volveremos más adelante con otras escalas a las que aplicaremos los mismos criterios de construcción de acordes. Como veremos, la armonización de cualquier modo de la escala mayor será una labor obvia, pero tendremos el placer de descubrir nuevos acordes cuando tratemos con escalas menores como la armónica o la melódica.

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2013/06/armonizacion-de-la-escala-mayor-7-ejercicios-finales/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice de todos los artículos de armonía.

Armonización de la escala mayor – 6: las tétradas

Objetivo: Deducir los acordes tétradas que aparecen al armonizar por terceras la escala mayor.

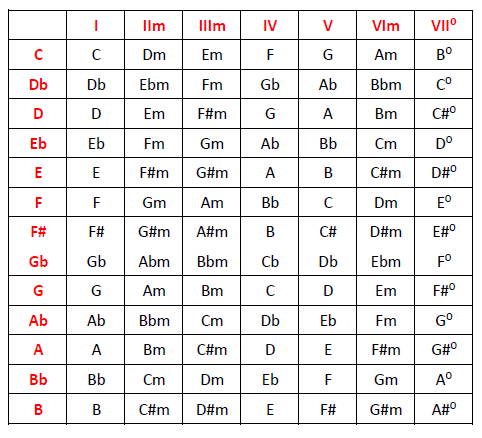
En los artículos anteriores aprendimos a armonizar la escala mayor superponiendo intervalos de terceras y dedujimos los acordes de tres notas (tríadas) que nos aparecían. Obtuvimos el siguiente paquete de acordes:

I – IIm – IIIm – IV – V – VIm – VIIº

en el que los números romanos hacen mención al grado de la escala correspondiente.

Hoy vamos a agregar otra tercera diatónica (es decir, perteneciente a la misma escala) para obtener acordes de cuatro notas, conocidos como tétradas o cuatríadas. Eso nos permitirá ampliar nuestro repertorio tonal con siete acordes nuevos de colorido diferente a su versión en tres notas.

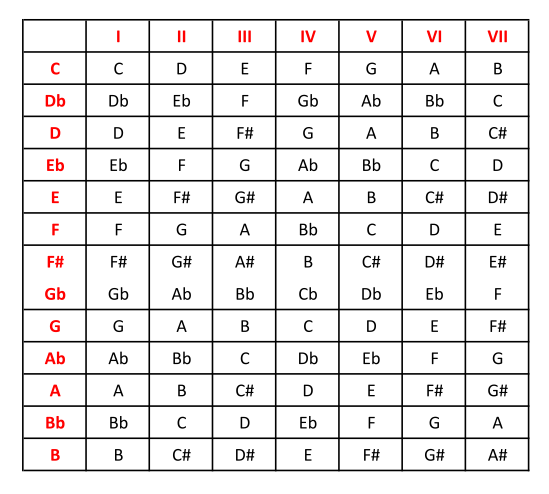
Utilizaremos para el cálculo la escala de Do mayor, generalizando después para el resto de las tonalidades mayores.

Do mayor: C – D – E – F – G – A – B – C

1) Acorde sobre el primer grado:

Partimos de la nota Do (C) y solapamos tres terceras.

C – E – G – B

Observa que un intervalo de tercera es equivalente a saltarse una nota y coger la siguiente.

Al igual que hicimos con las tríadas, descubramos la naturaleza de cada sucesiva tercera, es decir, indiquemos si es mayor (4 semitonos) o menor (3 semitonos).

De C a E: cuatro semitonos; tercera mayor.

De E a G: tres semitonos; tercera menor.

De G a B: cuatro semitonos; tercera mayor.

Tercera mayor + Tercera menor + Tercera mayor = acorde de séptima mayor (maj7 o 7M).

En nuestro caso, partiendo de C, el acorde es Do séptima mayor, Cmaj7.

Para entender mejor la aparición de esta séptima voy a ofrecerte un cálculo alternativo con el que conviene que estés familiarizado. En lugar de calcular el intervalo existente entre una nota y la anterior, vamos a hacerlo en relación a la primera nota del acorde, la fundamental.

Entre C y E, una tercera mayor, como ya hemos visto.

Entre C y G hay una quinta. Si cuentas los semitonos de diferencia obtienes siete, de modo que se trata de una quinta justa o perfecta.

[Si no tienes soltura calculando intervalos, puedo sugerirte la lectura de los ocho artículos de la serie Intervalos sin secretos, en el que se explica toda la teoría junto a numerosos ejemplos prácticos.]

Entre C y B hay una séptima. Se compone de 11 semitonos, de modo que es una séptima mayor.

Todos los intervalos nos han salido mayores, de modo que la fórmula de este acorde es:

1 – 3 – 5 – 7: acorde de séptima mayor, Cmaj7 en nuestro caso.

2) Acorde sobre el segundo grado:

Partimos de Re (D) y apilamos terceras:

D – F – A – C

Realizando las mismas cuentas que hicimos antes obtenemos la siguiente composición intervalica:

Tercera menor + Tercera mayor + Tercera menor = Acorde menor séptima (m7).

O bien, en relación a la fundamental:

1 – b3 – 5 – b7

En nuestro caso, sobre Re, Dm7.

3) Acorde sobre el tercer grado:

E – G – B – D

Tercera menor + Tercera mayor + Tercera menor : Acorde menor séptima (m7), como antes.

1 – b3 – 5 – b7

Con fundamental en Mi, Em7.

4) Acorde sobre el cuarto grado:

F – A – C – E

Tercera mayor + Tercera menor + Tercera mayor = acorde de séptima mayor (maj7 o 7M), el mismo tipo que sobre el primer grado.

1 – 3 – 5 – 7

Con fundamental en Fa, Fmaj7.

5) Acorde sobre el quinto grado:

G – B – D – F

Tercera mayor + Tercera menor + Tercera menor = acorde de séptima (7).

Calculando los intervalos en relación a la fundamental:

1 – 3 – 5 – b7

Observa que la séptima, a diferencia de lo que sucedía sobre el primer o cuarto grado, es menor. Ten presente que, a la hora de formar acordes, si no se especifica de qué tipo es la séptima, se está sobreentiendo que es menor. Sobre el primer y cuarto grados especificamos que la séptima es mayor, de ahí el nombre de los acordes: Do séptima mayor y Fa séptima mayor. Pero sobre el quinto grado la séptima es menor, y por eso decimos sólo Sol séptima, sin más calificativos.

Sobre Sol, pues, G7.

6) Acorde sobre el sexto grado:

A – C – E – G

Tercera menor + Tercera mayor + Tercera menor : Acorde menor séptima (m7), del mismo tipo que sobre los grados 2 y 3.

1 – b3 – 5 – b7

Sobre La, Am7.

En relación al comentario anterior, observa que no especificamos más que séptima, sin el adjetivo menor (el menor que precede al siete hace referencia a que la tercera es menor, propia de los acordes menores, y no califica la séptima, pues por defecto ya lo es). Existe un acorde menor semejante, pero con la séptima mayor, en lugar de menor, Am maj7 y se denomina La menor con séptima mayor. Lo veremos aparecer cuando armonicemos otro tipo de escalas.

7) Acorde sobre el séptimo grado:

B – D – F – A

Tercera menor + Tercera menor + Tercera mayor = Acorde menor séptima con quinta disminuida, conocido también como semidisminuido: m7(b5).

A veces, podrás encontrarte este acorde escrito de un modo diferente: el mismo circulito que empleábamos para los disminuidos, pero con una línea partiéndolo por la mitad: ∅

En relación a la fundamental,

1 – b3 – b5 – b7

Sobre Si, Bm7(b5).

Ya tenemos nuestros siete acordes buscados. Agrupémoslos:

Cmaj7 – Dm7 – Em7 – Fmaj7 – G7 – Am7 – Bm7(b5)

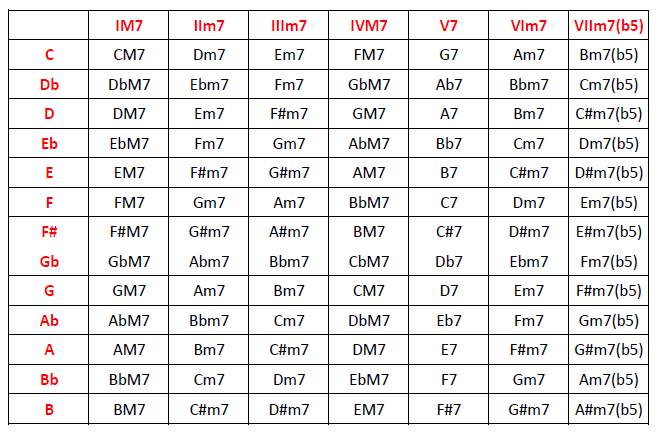
Generalizar al resto de tonalidades mayores es inmediato:

Imaj7 – IIm7 – IIIm7 – IVmaj7 – V7 – VIm7 – VIIm7(b5)

Conclusión: acordes de séptima mayor sobre los grados 1 y 4, menores séptima, sobre el 2, 3 y 6, séptima sobre el 5 (grado conocido como dominante, de ahí la forma común de referirse al acorde de séptima como acorde de séptima de dominante) y menor séptima con quinta bemol sobre el 7.

Al igual que con las tríadas, apréndete bien estos acordes, ingredientes con los que todo compositor prepara sus recetas mágicas.

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2013/05/armonizacion-de-la-escala-mayor-6-las-tetradas/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice de todos los artículos de armonía.

Armonización de la escala mayor – 5

Objetivo: mostrar ejemplos prácticos del cálculo de la familia de acordes tríada diatónicos.

Hemos llegado a una importante conclusión: en una tonalidad mayor cualquiera la familia de acordes tríadas diatónicos, es decir, los acordes de tres notas que nos aparecen utilizando los grados de la escala, responde a la siguiente estructura:

I – IIm – IIIm – IV – V – VIm – VIIº

O bien, empleando minúsculas para los acordes menores:

I – ii – iii – IV – V – vi – viiº

Memorizando esta relación y conociendo cómo se construye la escala mayor, es prácticamente inmediata la deducción de acordes diatónicos en cualquier tonalidad. Veamos algunos ejemplos.

Supongamos que quiero componer una canción en Re mayor, ¿qué acordes tríada inmediatos tengo a mi disposición?

Comenzamos construyendo la escala de Re mayor:

Re mayor: D – E – F# – G – A – B – C# – D

De modo que los acordes buscados son:

D – Em – F#m – G – A – Bm – C#º

No hay más misterio, así de sencillo.

Otro ejemplo: deduzcamos los acordes diatónicos de Fa mayor.

Fa mayor: F – G – A – Bb – C – D – E – F

F – Gm – Am – Bb – C – Dm – Eº

A veces las preguntas pueden tomar formas distintas…

Has compuesto una canción para tu banda en Mi bemol mayor y el bajista te pregunta si el Do es mayor o menor.

Construímos la escala de Mi bemol mayor:

Mi bemol mayor: Eb – F – G – Ab – Bb – C – D – Eb

De modo que los acordes diatónicos son:

Eb – Fm – Gm – Ab – Bb – Cm – Dº

Contéstale al bajista que el acorde es Do menor; que cuide la tercera en su groove sobre ese acorde. Recomiéndale también que estudie algo de armonía.

En la siguiente entrega extenderemos nuestra querida familia de acordes diatónicos deduciendo las tétradas o cuatríadas, acordes de cuatro notas. Eso ampliará tu abanico de opciones ofreciéndote la posibilidad de enriquecer y dar otro colorido a tus creaciones.

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2013/05/armonizacion-de-la-escala-mayor-5/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice de todos los artículos de armonía.

Armonización de la escala mayor – 4

Objetivo: observar que el tipo de acorde que se obtiene al armonizar la escala mayor depende del grado concreto y no de la tonalidad.

En el anterior artículo descubrimos los acordes que aparecían al armonizar la escala de Do mayor:

C – Dm – Em – F – G – Am – B°

Esto es, obtenemos acordes mayores en los grados primero, cuarto y quinto, menores en el segundo, tercero y sexto y disminuido en el séptimo grado.

Voy a plantearte una cuestión que probablemente podrás responder ya. Imagínate que realizamos la misma operación sobre otra escala mayor diferente a Do mayor como, por ejemplo, La mayor. ¿De qué tipo crees que serán los acordes que nos aparecerán?

Todas las escalas mayores comparten una característica común, que es su estructura interválica. Recuerda su fórmula:

T – T – S – T – T – T – S

La distancia que cada grado mantiene respecto al primero (denominado tónica), comparando entre otras escalas mayores, es siempre la misma, tanto si se trata de Do mayor, La mayor o Mi bemol mayor. Es de esperar, por lo tanto, que los acordes que obtengamos al armonizar sean de la misma especie también.

Calculemos los acordes que se derivan de la escala La mayor aplicando la metodología que empleamos para Do mayor.

Si aplicamos la fórmula interválica de la escala mayor partiendo de la nota La (A), obtenemos:

La mayor: A – B – C# – D – E – F# – G# – A

Si armonizamos por terceras nos aparecen los siguientes acordes de tres notas (tríadas):

A –> A – C# – E –> tercera mayor + tercera menor –> A

B –> B – D – F# –> tercera menor + tercera mayor –> Bm

C# –> C# – E – G# –> tercera menor + tercera mayor –> C#m

D –> D – F# – A –> tercera mayor + tercera menor –> D

E –> E – G# – B –> tercera mayor + tercera menor –> E

F# –> F# – A – C# –> tercera menor + tercera mayor –> F#m

G# –> G# – B – D –> tercera menor + tercera menor –> G#°

Comparemos esta nueva familia de acordes con la que obtuvimos de Do mayor:

Do mayor: C – Dm – Em – F – G – Am – B°

La mayor: A – Bm – C#m – D – E – F#m – G#°

Como puedes ver, pese a ser, naturalmente, diferentes, mantienen el tipo, como campeones, grado a grado: mayores sobre el primero, cuarto y quinto, menores sobre el segundo, tercero y sexto, y disminuido sobre el séptimo.

Esta importante conclusión podemos reflejarla así, indicando cada grado por números romanos:

I – IIm – IIIm – IV – V – VIm – VII°

Memorízala bien, pues te ayudará a manejarte con soltura cuando tengas que lidiar con tonalidades distintas.

En muchas publicaciones esta misma relación aparece escrita del siguiente modo:

I – ii – iii – IV – V – vi – vii°

Conviene que te familiarices también con ella.

La diferencia estriba en que los acordes menores los indicamos directamente con el grado escrito en minúsculas, sin necesidad de recurrir al sufijo m. El acorde sobre el séptimo grado también está en minúsculas, pese a que no sea estrictamente menor, pues la distancia entre su fundamental y tercera es una tercera menor, intervalo característico de todos los acordes menores.

Todo lo escrito hasta ahora en esta serie no tenía otra misión sino llegar a la conclusión fundamental que acabamos de deducir, herramienta imprescindible para todo compositor o arreglista. En el próximo artículo realizaremos algunos ejercicios prácticos que ilustrarán su aplicación.

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2013/05/armonizacion-de-la-escala-mayor-4/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice de todos los artículos de armonía.

Armonización de la escala mayor – 3

Objetivo: nombrar los acordes tríadas resultado de armonizar por terceras la escala de Do mayor.

En la segunda entrega de la serie aprendimos a deducir los acordes de tres notas (tríadas) que se obtenían al apilar terceras sobre las notas de la escala de Do mayor. En el artículo de hoy nos ocuparemos de ponerles nombre.

Recuperemos, en primer lugar, la tabla que obtuvimos al armonizar Do mayor:

DO: DO – MI – SOL (C – E – G)

RE: RE – FA – LA (D – F – A)

MI: MI – SOL – SI (E – G – B)

FA: FA – LA – DO (F – A – C)

SOL: SOL – SI – RE (G – B – D)

LA: LA – DO – MI (A – C – E)

SI: SI – RE – FA (B – D – F)

Pese a que todos los acordes los hemos obtenido apilando terceras, no todos mantienen la misma distancia entre sus notas (intervalos).

Observa, por ejemplo, el primero, construido sobre la nota DO:

DO – MI – SOL

Entre DO y MI, ¿cuántos semitonos hay? Contemos:

DO#, RE, RE#, MI; 4 semitonos (a la hora de contar semitonos NO incluimos la nota inicial).

Una tercera con una distancia de 4 semitonos se denomina tercera mayor.

Toma ahora el siguiente intervalo de tercera del mismo acorde. Veamos qué distancia hay entre MI y SOL.

FA, FA#, SOL; 3 semitonos

A este tipo de tercera, con una distancia de 3 semitonos, se la conoce como tercera menor.

Podemos concluir, por lo tanto, que el acorde DO – MI – SOL es el resultado de superponer sobre la nota DO una tercera mayor seguida de otra menor.

Analicemos el siguiente acorde de la lista y comprobemos que la situación es la opuesta:

RE – FA – LA

¿Qué distancia hay entre RE y FA?

RE#, MI, FA; 3 semitonos. Entre RE y FA hay una tercera menor.

¿Y entre FA y LA?

FA#, SOL, SOL#, LA; 4 semitonos. Entre FA y LA hay una tercera mayor.

De modo que el acorde RE – FA – LA se obtiene de superponer, sobre la nota RE, una tercera menor seguida de otra mayor.

Justo lo contrario de lo que ocurría en el primer acorde. Es precisamente esa diferencia la que determina el nombre del acorde.

A la hora de apilar terceras nos pueden suceder los siguientes casos:

– tercera mayor + tercera menor = acorde mayor
– tercera menor + tercera mayor = acorde menor
– tercera menor + tercera menor = acorde disminuido
– tercera mayor + tercera mayor = acorde aumentado

Naturalmente, cuando usamos la palabra acorde, nos estamos refiriendo al acorde tríada, compuesto de tres notas. Más adelante realizaremos el estudio para las tétradas o cuatríadas.

Con este sencillo esquema podemos ya nombrar cada acorde:

DO: DO – MI – SOL; tercera mayor + tercera menor

Por lo tanto, se trata del acorde Do mayor, que en cifrado moderno se representa por C (la nota fundamental del acorde sin ningún calificativo más).

RE: RE – FA – LA; tercera menor + tercera mayor

Estamos ante RE menor, representado por Dm (la fundamental D, seguida del calificativo m o min).

MI: MI – SOL – SI

Distancia entre MI y SOL, 3 semitonos; distancia entre SOL y SI, cuatro semitonos.

Tercera menor + tercera mayor; acorde menor. Mi menor, Em

FA: FA – LA – DO

Distancia entre FA y LA, 4 semitonos. Entre LA y DO, 3 semitonos.

Tercera mayor + tercera menor; acorde mayor: F

SOL: SOL – SI – RE

Distancia entre SOL y SI, 4 semitonos. Entre SI y RE, 3 semitonos. Acorde mayor, nuevamente: G

LA: LA – DO – MI

Distancia entre LA y DO, 3 semitonos. Entre DO y MI, 4 semitonos. Acorde menor, Am

SI: SI – RE – FA

Distancia entre SI y RE, 3 semitonos. Entre RE y FA, 3 semitonos también.

Tercera menor + tercera menor; acorde disminuido: B dim, o bien, Bº

Ya tenemos nuestra flamante colección de tríadas resultado de armonizar por terceras la escala de Do mayor:

C – Dm – Em – F – G – Am – Bº

Estos son nuestros siete acordes diatónicos buscados. La gran, gran mayoría de las canciones escritas en Do mayor contienen exclusivamente estos acordes. Y si hay alguno ajeno a esta relación suele ser en pinceladas controladas que aportan un toque peculiar a la composición. Date cuenta de que cualquier otro acorde tríada que no sea uno de estos siete contendrá, al menos, una nota no diatónica, es decir, una nota que no pertenecerá a la escala de Do mayor.

En la siguiente entrega analizaremos otra tonalidad cualquiera y generalizaremos las conclusiones.

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2013/04/armonizacion-de-la-escala-mayor-3/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice de todos los artículos de armonía.

Armonización de la escala mayor – 2

Objetivo: armonizar la escala de Do mayor y deducir las tríadas diatónicas que se generan.

En el primer artículo de esta serie concluímos que nuestra primera opción a la hora de armonizar una melodía escrita en una tonalidad mayor era emplear acordes diatónicos, es decir, con notas pertenecientes a la propia tonalidad.

Dijimos que la gran mayoría de las composiciones estaban basadas en progresiones de acordes diatónicos, que ocasionalmente se complementaban con otros ajenos que contribuían a darle un carácter peculiar a la creación.

Vamos a descubrir ahora qué acordes son esos, comenzando, en primer lugar, por las estructuras más simples: los acordes de tres notas, las tríadas. Una vez entendidas estas ampliaremos el estudio a los acordes de cuatro notas (cuatríadas o tétradas).

Por sencillez, comenzaremos armonizando la escala diatónica por excelencia, Do mayor. Sus notas se hallan en las teclas blancas de un piano, de modo que no tiene alteraciones (los bemoles o sostenidos que representan las teclas negras). Como veremos, las conclusiones a las que lleguemos armonizando esta escala serán perfectamente aplicables a otras tonalidades mayores.

Tomemos nuestra escala de Do mayor, la secuencia universal

DO – RE – MI – FA – SOL – LA – SI – DO

y construyamos acordes (armonicemos) sobre cada una de esas notas.

La forma más común de armonizar una escala consiste en superponer terceras diatónicas. Existen otros modos más exóticos de hacerlo, pero son mucho menos habituales y no hablaremos de ellos en esta serie.

Superponer terceras no significa otra cosa que ir añadiendo notas que estén a una distancia sucesiva de una tercera una de otra.

[Si no tienes claro el concepto de tercera te sugiero que leas la serie de siete artículos dedicados al cálculo de intervalos, exhaustiva y con numerosos ejemplos prácticos. No obstante, procuraré referir aquí los puntos más esenciales, de modo que puedas seguir avanzando en la lectura aunque no dispongas de esos fundamentos básicos.]

Comencemos por la primera nota de la escala, DO, la tónica.

Para contar una tercera diatónica, contamos secuencialmente tres notas, incluyendo la inicial, y usando sólo notas de esa escala (de ahí la denominación diatónica): DO (1), RE(2), MI(3). La nota buscada es MI.

Agreguemos ahora una nueva tercera a partir de MI: MI(1) – FA(2) – SOL(3); es decir, SOL.

De modo que sobre la primera nota, DO, hemos construido nuestro primer acorde:

DO – MI – SOL

Aunque te anticipo que este acorde se denomina Do mayor, prefiero demorar la nomenclatura hasta que hayamos desglosado la composición de los restantes.

Realicemos la misma operación en las demás notas de la escala. La siguiente tabla resume el cálculo (las notas escritas en mayúsculas resaltan las terceras):

DO: DO – re – MI – fa – SOL —> DO – MI – SOL (C – E – G, en notación anglosajona)

RE: RE – mi – FA – sol – LA —> RE – FA – LA (D – F – A)

MI: MI – fa – SOL – la – SI —> MI – SOL – SI (E – G – B)

FA: FA – sol – LA – si – DO —> FA – LA – DO (F – A – C)

SOL: SOL – la – SI – do – RE —> SOL – SI – RE (G – B – D)

LA: LA – si – DO – re – MI —> LA – DO – MI (A – C – E)

SI: SI – do – RE – mi – FA —> SI – RE – FA (B – D – F)

Asegúrate de que entiendes perfectamente el proceso realizado. Te propongo, como ejercicio, que realices estos mismos cálculos en otras tonalidades. Por ejemplo, toma Fa mayor (F – G – A – Bb – C – D – E – F) y deduce qué notas constituyen los acordes tríadas que aparecen al armonizar.

La siguiente imagen muestra gráficamente la armonización de Do mayor en un pentagrama. Es útil, aunque no conozcas nada de solfeo, visualizar espacialmente esta apilación de notas.

Ya tenemos la composición de cada acorde; ahora tan sólo nos falta nombrarlos adecuadamente. ¿De qué tipo son? ¿Cuáles son mayores y cuáles menores? En breve estaremos en condiciones de responder a estas preguntas.

Javier Montero Gabarró

Armonización de la escala mayor – 2

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice de todos los artículos de armonía.

Armonización de la escala mayor – 1

Objetivo: presentar la serie dedicada a la armonización de la escala mayor y entender el concepto de acorde diatónico.

En la vida de todo músico, particularmente si se tiene interés en la composición, hay un hito formativo que marca un claro antes y después: el conocimiento de la armonización de la escala mayor.

Recuerdo mis primeros pinitos en la guitarra tratando de descubrir los acordes de las canciones que me gustaban. En buena parte se trataba de una cuestión de ensayo y error entre todos los acordes que me conocía hasta que encontraba alguno que parecía atinar.

Mis primeras composiciones también eran un tanto caóticas. Mezclaba acordes sin ton ni son y trataba de encontrar melodías que se ajustaran a ellos. Mis únicas guías eran la intuición y ver cómo lo hacían otros y, aunque en música la intuición es siempre la mejor de las guías, tener cierta conciencia de lo que uno está haciendo facilita las cosas y puede ayudarte en el proceso creativo.

Tal vez te hayas planteado en alguna ocasión cuestiones como estas:

«Quiero escribir una canción en Sol menor, ¿qué acordes puedo utilizar?»

«Estando en la tonalidad de Fa mayor, ¿puedo usar un acorde de La mayor?»

Estas preguntas tienen truco, desde luego… En música puedes usar las notas y acordes que te dé la gana. El gran músico y profesor Jamie Aebersold solía decir que no hay notas equivocadas, sólo pobres elecciones. Lo cierto es que debes hacerte responsable de tus decisiones y, hasta cierto punto, del efecto que estas provoquen en quien te escuche.

El hecho de optar por una tonalidad concreta ya lleva implícito un conjunto de notas «seguras» sobre las que nos apoyaremos para construir la melodía y armonía. Son seguras en el sentido de que son las que nuestros oídos, educados durante tanto tiempo en nuestro sistema tonal occidental, aceptarán sin discusión.

Si, por ejemplo, vamos a componer una canción en Fa mayor, esas notas seguras no son otras sino las que corresponden a la escala del mismo nombre:

Fa mayor: Fa – Sol – La – Si bemol – Do – Re – Mi – Fa

[Si no sabes construir esta escala, permíteme que te sugiera la lectura del artículo del blog en el que explico cómo construir la escala mayor en cualquier tonalidad.]

De entre las doce notas existentes en nuestro sistema musical, hemos elegido un subconjunto de siete concretas. Una melodía escrita en Fa mayor está centrada en una nota principal, Fa, denominada la tónica, alrededor de la cual bailan las restantes de la escala.

¿Qué acordes debo utilizar, por lo tanto, si quiero armonizar una melodía escrita en Fa mayor?

La respuesta es muy sencilla: aquellos que están compuestos de notas que pertenecen a la escala de Fa mayor.

La mayoría de nuestra música occidental está escrita así, empleando una escala diatónica de 7 notas armonizada por acordes derivados de la misma escala.

Estos acordes, a los que nos referiremos de ahora en adelante como diatónicos, son los que funcionan, la apuesta segura si queremos que nuestra música sea aceptada con facilidad.

Ahora bien, limitar la creación musical a únicamente el empleo de escalas y acordes diatónicos es ponerle rejas a nuestra creatividad. Como niños desobedientes, nos gusta desafiar al sistema tonal introduciendo notas y acordes non gratos en nuestras melodías y armonías. Eso nos hace sentirnos más libres (aunque, en el fondo, sigamos siendo prisioneros) y nuestras composiciones pueden resultar más interesantes.

Hace mucho que no escribo una canción con acordes completamente diatónicos (aunque siempre supone un buen reto hacerlo) y, camuflado entre la mafia de acordes de la tonalidad, suelo colar algún que otro infiltrado, buscando hacer sentir algo especial al oyente.

A lo largo de la serie de Armonía del blog aprenderemos algunas categorías de acordes no diatónicos que podemos infiltrar fácilmente y que, con el paso del tiempo, han sabido ganarse ya el respeto de nuestros oídos y son aceptados como si fueran de la familia. Pero antes de eso has de invertir tiempo conociendo el universo diatónico.

De modo que tu primera labor como compositor no es otra sino conocer cuáles son esos acordes diatónicos pues, a no ser que tires por otros derroteros, como por ejemplo la música atonal, constituirán la gran mayoría de los acordes que utilizarás en tus creaciones. De ellos hablaremos precisamente en la saga de artículos que hoy comienza.

Antes de aprender qué acordes son esos, conviene que te familiarices con el ejercicio inverso y realices algunos ejercicios como los siguientes:

– Estando en la tonalidad de Fa mayor, ¿puedo usar el acorde La mayor?

Ya hemos visto que la pregunta, tal como está planteada, es poco afortunada, de modo que replanteémosla:

¿Es el acorde La mayor diatónico de la tonalidad de Fa mayor?

Para responder a esa pregunta basta con descomponer el acorde La mayor en sus notas simples y comprobar si pertenecen a la escala Fa mayor, es decir, a la escala

Fa mayor: F – G – A – Bb – C – D – E – F

El acorde tríada La mayor es:

La mayor: A – C# – E

Como ves, la tercera del acorde, C# no forma parte de la escala. Por lo tanto La mayor no es un acorde diatónico en esa tonalidad.

Sin embargo, La menor (A – C – E) sí que lo sería. En un tema escrito en Fa mayor el acorde La menor siempre sonará de perlas.

[Si no sabes descomponer un acorde en sus notas constituyentes, puedes echarle un vistazo a la serie Construcción de acordes, en la que se desgrana cada tipo de acorde, desde los más simples como las tríadas hasta los más complejos con cinco o más notas.]

– En la tonalidad de Do mayor, ¿es Fmaj7 un acorde diatónico?

La escala:

Do mayor: C – D – E – F – G – A – B – C

El acorde:

Fmaj7: F – A – C – E

Todas sus notas están incluidas en la escala de Do mayor, de modo que le ponemos la pegatina con el visto bueno.

En cambio, un acorde de séptima, F7, ya no lo sería, pues incorpora un Eb en lugar de E.

Ejercítate tú mismo con otras escalas y acordes.

En el próximo artículo descubriremos qué acordes, en su versión más simple, las tríadas, son los diatónicos de Do mayor (la más fácil de las escalas mayores) y extraeremos conclusiones extrapolables al resto de las tonalidades mayores.

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2013/04/armonizacion-de-la-escala-mayor-1/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice de todos los artículos de armonía.

Etiqueta: escala mayor

La escala mayor en las 12 tonalidades – Cuadro

Armonización de la escala mayor en las 12 tonalidades

La fórmula relativa de los modos de la escala mayor

Armonización de la escala mayor – 7: Ejercicios finales

Armonización de la escala mayor – 6: las tétradas

Armonización de la escala mayor – 5

Armonización de la escala mayor – 4

Armonización de la escala mayor – 3

Armonización de la escala mayor – 2

Armonización de la escala mayor – 1

Uso de cookies

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Uso de cookies