 Objetivo: mostrar las fórmulas de la escala de tonos enteros y algunas de sus aplicaciones.
Objetivo: mostrar las fórmulas de la escala de tonos enteros y algunas de sus aplicaciones.
Si hay una escala fácil de aprender además de la cromática, en la que el intervalo de separación entre notas contiguas es siempre un semitono, esta es sin duda la escala de tonos enteros, en la que la distancia entre notas tiene el valor fijo de un tono (2 semitonos).
Si la fórmula absoluta de la escala cromática es
S – S – S – S – …,
la fórmula de la escala de tonos enteros es
T – T – T – T – …
Imposible olvidarla.
Vamos a construirla a partir de Do, lo que nos servirá para deducir su fórmula relativa y para apreciar ciertas particularidades.
Comenzamos por Do: C
Un tono por encima es Re: D
Un tono sobre Re está Mi: E
Y ahora, puesto que entre Mi y Fa hay sólo un semitono, un tono por encima de Mi es Fa sostenido: F#
Si agregamos un tono a Fa# obtenemos Sol# (G#).
Un tono sobre Sol# es La# (A#).
Finalmente, un tono por encima de La# se encuentra Do nuevamente, ya que el intervalo entre Si y Do es sólo de un semitono.
Recopilemos esta colección de notas:
C – D – E – F# – G# – A# – C
Lo primero que debes constatar, sin tener en cuenta la repetición del último Do (una octava más alto), es que la escala dispone únicamente de seis notas, en contraposición a las siete que componen las escalas diatónicas a las que estamos acostumbrados. Esto no debería ser una sorpresa: si nuestro sistema musical consta de 12 notas y las espaciamos uniformemente a una distancia de 2 semitonos, obtenemos doce dividido entre dos, seis notas en la escala.
La segunda observación importante es que, en realidad, únicamente hay dos escalas de tonos enteros. Repitamos el cálculo de la inmediatamente siguiente, es decir, partiendo desde Do#:
C# – D# – F – G – A – B – C#
La siguiente sería sobre Re:
D – E – F# – G# – A# – C – D
Pero, si te fijas, verás que tiene exactamente las mismas notas que la que construimos sobre Do. Y lo mismo te ocurrirá si construyes ahora la de Re#: idéntica a Do#.
Y no podemos decir que se trate de modos diferentes. Al contrario de lo que sucede con los modos griegos derivados de la escala diatónica de Do mayor, que pese a tener las mismas notas presentan fórmulas distintas y, por lo tanto, intervalos diferentes entre grado y grado, la escala de tonos enteros es completamente plana y muestra la misma fórmula tanto si la empiezas en Do como si lo haces en Re (o en Fa#, Sol#, etc.).
De modo que sólo dos escalas, lo que hace que sea tremendamente sencilla de aprender en cualquier instrumento.
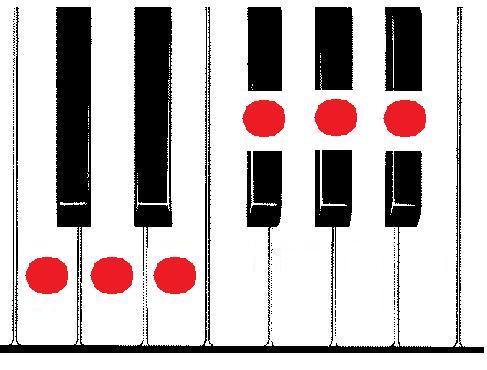
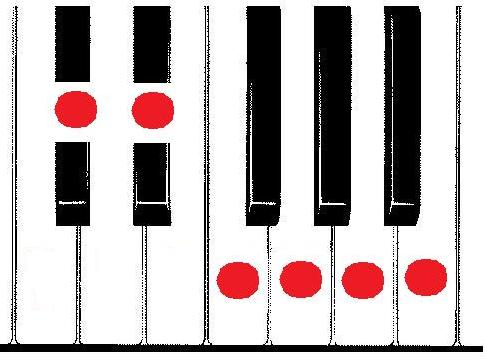
Veamos las dos posiciones en un piano:
Vamos a dividir cada octava en dos zonas: 1) las notas entre Do y Mi y 2) las notas entre Fa y Si, ambas con sus correspondientes blancas y negras.
Pues bien, la primera escala de tonos enteros la obtienes tocando todas las notas blancas de la zona 1 y todas las negras de la 2.
A su vez, la segunda forma de la escala se construye de modo inverso: tocando todas las negras de la zona 1 y las blancas de la 2.
Y no hay más variedades; escala aprendida.
Para deducir la fórmula relativa de nuestra protagonista debemos compararla con la referencia Do mayor:
Do mayor:
C - D - E - F - G - A - B
1 - 2 - 3 - 4 - 5 - 6 - 7Do, tonos enteros:
C - D - E - F# - G# - A#
de modo que sus grados son:
1 - 2 - 3 - #4 - #5 - #6El primer gráfico de la escala en el piano, partiendo de Do, ilustra perfectamente esta fórmula.
¿En qué contexto suele utilizarse la escala de tonos enteros?
Para responder a esta pregunta vamos a reescribirla de este otro modo, en el que simplemente hemos cambiado algunos sostenidos por sus correspondientes bemoles enarmónicos:
1 – 2 – 3 – b5 – #5 – b7
¿Qué acordes pueden beneficiarse de estos grados?
El primer vistazo hay que echarlo siempre sobre la tercera y la séptima. En nuestra escala la tercera es mayor (3) y la séptima menor (b7), lo que hace pensar en los acordes de séptima dominante.
Fíjate ahora en la quinta. No la encuentras perfecta, sino aumentada o disminuida.
De modo que ya lo tienes: la escala de tonos enteros es una buena opción para construir melodías sobre acordes dominantes alterados, tanto si la alteración consiste en disminuir la quinta como en aumentarla. Es un recurso a tener siempre en cuenta al improvisar en jazz sobre este tipo de acordes.
Tal vez el ejemplo más popular de su uso en la música pop sea en la Intro de la genial canción de Stevie Wonder You are the sunshine of my life. Inconfundible ese ascenso por la escala de tonos enteros armonizada en terceras al comienzo del tercer compás, justo cuando la armonía perfila el acorde de dominante alterado (G7#5 si estás tocando en Do mayor). El enlace al que apunta el título de la canción ilustra cómo tocar la intro en el piano.
Con esa melodía resonando te dejo hasta la siguiente entrega. Hasta entonces, canta y sé feliz.
Javier Montero Gabarró
http://elclubdelautodidacta.es/wp/2013/08/la-escala-de-tonos-enteros/
El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)
El Club del Autodidacta
Índice completo de artículos sobre armonía.

Qué maravilla de artículos escribes Javier, da gusto la elegancia y el esfuerzo por explicarlo todo de forma óptima y con sinceras intenciones de que el lector aprenda. Gracias una vez más. José Guzmán
Bueno, debo decir que he disfrutado mucho escribiendo el artículo. Cuando le pones pasión e ilusión a tu trabajo es más probable que obtengas buenos resultados. 🙂
Gracias, Jose.
lo mejor de lo mejor que he encontrado, muchas gracias por su amable y valiosa aportacion
Me alegro de que te haya sido útil, María.
¡Gracias por tus palabras!
Que bien bro, excelente!
Una pregunta, respondes dudas sobre armonía funcional y atonal?
Un fuerte abrazo.
¡Gracias, Eduardo!
Mi visión de la armonía funcional es un tanto pragmática, y siempre desde el lado del músico más que del teorizador. Desconfío de los modelos que se esfuerzan en restringir o justificar nuestra experiencia musical. Tomo de ellos lo que me interesa y cuando me interesa, pero no tengo el menor escrúpulo en obviarlos cada dos por tres.
Pero, por supuesto, hablaremos de armonía funcional en el blog, así como de la música atonal (un campo fascinante). También me gustaría incidir en música microtonal, un terreno que estoy comenzando a investigar gracias al progreso del software, que te da herramientas para hacer lo que quieras con los sonidos.
Esto no ha hecho más que empezar.
La música es un campo infinito por explorar. Todo intento de someterla a reglas no es más que una trampa para la creatividad.
Saludos
Quería saber obras, aparte de la citada de Wonder, que usen esta escala, sean clasicas u otras. ¿Como generan la tension y relajación?
Buenos días, Juan:
En la Wikipedia (busca «whole tone scale») podrás encontrar algunos ejemplos de piezas que incluyen frases en esa escala, tanto en en la composición clásica como moderna.
Esta escala es usada ampliamente especialmente en el jazz a la hora de improvisar sobre determinados acordes. Dado que es rica en vitamina b5 y #5 es un recurso fantástico para acordes alterados, por ejemplo. Sobre la tensión/relajación, piensa que esta escala es una invitada ocasional en una pieza y, aunque se trate de un invitado realmente ameno, interesante y entretenido para la audiencia, como invitada que es no le corresponde la responsabilidad de la satisfacción global, labor que recae sobre su anfitrion. Dicho de otro modo más claro: esta escala, se usa, sobre todo para generar tensión sobre acordes tensos. Que sean otros acordes y escalas los que se ocupen de restablecer la paz.
Saludos
Porque solamente hay dos escalas de tonos enteros?
Una forma de verlo geométricamente es la siguiente. Considera un círculo (un reloj, por ejemplo) dividido uniformemente en doce marcas (las horas del reloj). En cada marca colocas una nota: Do a las 12, Do# a la 1, Re a las 2, y así sucesivamente, hasta las 11, en la que estaría la nota SI. Esta similitud es posible porque nuestra escala tiene 12 notas, igual que las 12 horas del reloj.
Ahora, a partir de la nota DO, redondea las notas que forman la escala de tonos enteros. Si empezamos por DO, la siguiente es RE, pues hay un tono de separación. Es decir, te saltas una hora y redondeas la siguiente. Así obtendrías tu primera escala con las seis notas siguientes: C – D – E – F# – G# – A#.
Repite el procedimiento pero empezando ahora por la nota C#, saltándote «una hora» y tomando la siguiente. La escala que obtienes sería: C# – D# – F – G – A – B.
Ahora prueba a empezar por cualquier otra nota: comprobarás que las notas que obtienes, en cualquier caso, son las mismas que en alguna de las dos escalas que ya has calculado. Además, las relaciones interválicas entre cualquier par de notas son siempre las mismas, empieces por donde empieces.
Saludos
que vaina tan buena, me lo aprendi al vuelo… pero sigo con la duda sobre los acordes dominantes!!
Bro estupenda clase, me ha quedado muy clara la manera de armonizarla. o mas bien de aplicarla sobre ciertos acordes 🙂
justo hoy estoy estudiando sobre esta escala ya que un amigo canta una melodía usándola y en el tema que estamos produciendo en conjunto me gustaría poder aprovechar mejor esta sonoridad, muchas gracias