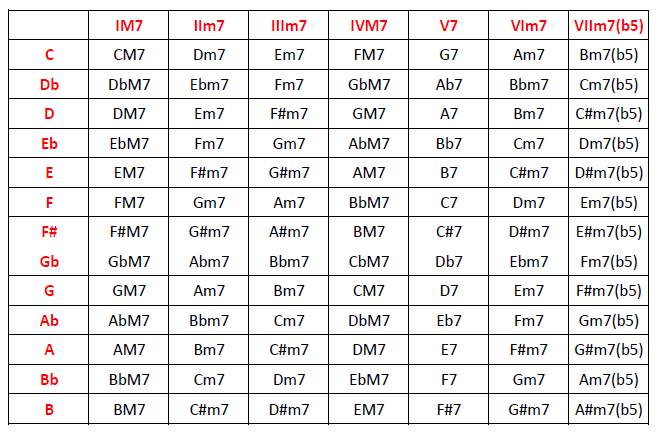
Objetivo: aprender el concepto de inversión de un acorde.
Objetivo: aprender el concepto de inversión de un acorde.
Es importante distinguir entre la fórmula de un acorde, que no es más que una descripción de las notas que deben formar parte de él, y la disposición concreta que el instrumentista elige para hacerlo sonar. Para poder diferenciar sin ambigüedad ambos modos de referirnos a un acorde, ideamos la notación estructural de voces.
Una inversión es, en esencia, un tipo de disposición particular de las voces del acorde.
Para entender el concepto, elijamos un acorde sencillo, como la tríada mayor:
Mayor: 1 - 3 - 5
La disposición más básica para construir este acorde coincide con su fórmula:
[1, 3, 5]
El instrumentista hace sonar sólo tres notas, sin repetirlas, ordenándolas del modo que está indicado entre los corchetes: la más grave es la fundamental, la siguiente la tercera y la más aguda la quinta, todo comprendido en el ámbito de una octava.
Para invertir el acorde, tomemos la más grave -en este caso, la fundamental- y llevémosla, subiéndola una octava, a la derecha del todo, convirtiéndola así en la más aguda. La disposición resultante es la siguiente:
[3, 5, 1]
Observa que ahora la más grave es la tercera del acorde, a la que sigue la quinta, exponiendo la fundamental como voz más aguda de la disposición.
A esta manera concreta de organizar el acorde la denominamos primera inversión de la tríada mayor.
Quizás el término más adecuado para esto sería rotación en lugar de inversión, pues lo que hemos hecho ha sido rotar las notas, no invertirlas. En cualquier caso, quédate con la terminología aceptada: la primera inversión deja la tercera como voz más grave.
Veamos una aplicación práctica de esto en el piano y en la guitarra. Consideremos por ejemplo, el acorde Do mayor [DO, MI, SOL] y su primera inversión [MI, SOL, DO]. Acompañamos su representación en el pentagrama también, pues es bastante ilustrativa de la recolocación de las notas:


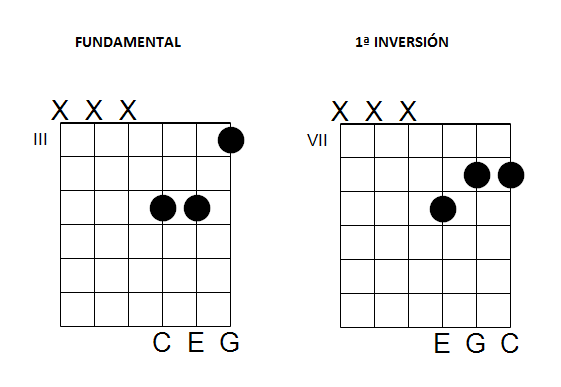
Haz sonar ambos acordes y diferencia su cualidad sonora. La distinta colocación de las notas implica la aparición de nuevos intervalos. En particular, aprecia el intervalo de cuarta justa característico que se forma entre la quinta y la fundamental, situada ahora como primera voz (las voces se numeran comenzando por la más aguda).
Si partimos de la primera inversión de la tríada mayor y realizamos una nueva rotación de notas, llevando nuevamente la más grave a la derecha del todo, obtenemos su segunda inversión:
Tríada mayor: [1, 3, 5]
Tríada mayor en primera inversión: [3, 5, 1]
Tríada mayor en segunda inversión: [5, 1, 3]Volviendo al ejemplo de Do mayor en disposición [1, 3, 5], [DO, MI, SOL], la segunda inversión es, por lo tanto, [SOL, DO, MI].
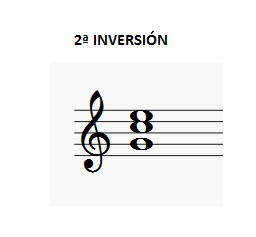
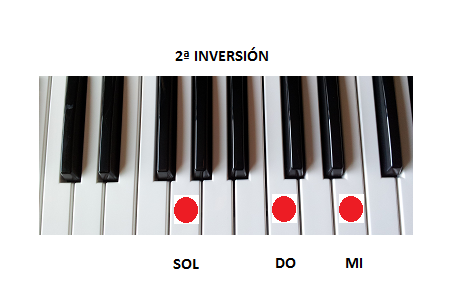
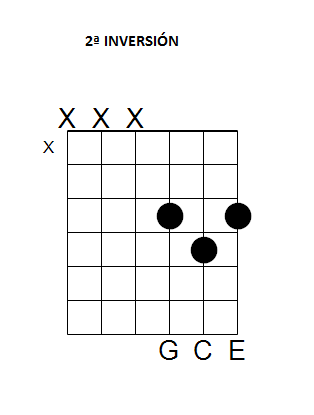
Observa que ahora la nota más grave es la quinta. Ese es el rasgo característico de la segunda inversión. Aprecia que aparece nuevamente el intervalo de cuarta entre la quinta y la fundamental, pero esta vez desplazado a la base del acorde.
Aplicando los mismos principios podemos invertir también los acordes de más de tres notas. Por ejemplo, consideremos la tétrada del acorde de séptima de dominante, de fórmula:
Séptima: 1 - 3 - 5 - b7
Posición fundamental cerrada: [1, 3, 5, b7]
Primera inversión: [3, 5, b7, 1]
Segunda inversión: [5, b7, 1, 3]Ya que contamos con una nota más, podemos contemplar una nueva rotación para alcanzar la tercera inversión, en la que la séptima es ahora la voz más grave:
Tercera inversión: [b7, 1, 3, 5]
En la práctica, es común hacer extensivo el concepto de inversión basándonos directamente en la voz más grave, independientemente de cómo se dispongan las notas a continuación. Decimos, por lo tanto, que un acorde está en primera inversión cuando su nota más grave es la tercera; en segunda inversión cuando lo es la quinta y en tercera inversión cuando descansa sobre la séptima.
El siguiente acorde, tan común entre guitarristas, representa un ejemplo de primera inversión de la tríada menor, 1 – b3 – 5:
[b3, 1, 5, 1]
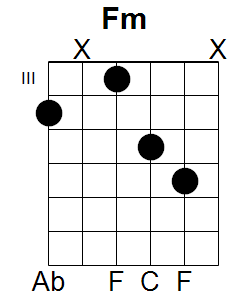
Con frecuencia, el compositor o arreglista desea reflejar que un determinado acorde se halla invertido -tal vez para matizar una línea de bajo en la armonía. En cifrado moderno esto se indica anotando, a continuación del acorde, separado por una barra inclinada, el nombre de la nota más grave.
En el ejemplo anterior, Fa menor en primera inversión, podemos representar el acorde como Fm/Ab. Esto indica que se trata de un Fa menor en el que la nota más grave es La bemol, que es precisamente la tercera del acorde.
Más ejemplos:
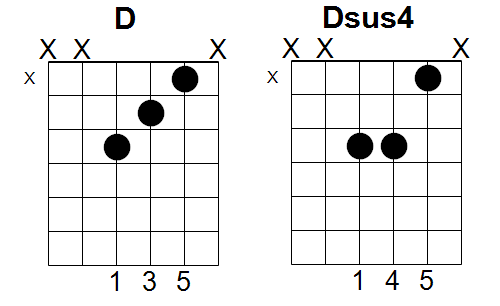
D/F# : Re mayor en primera inversión
Cmaj7/G : Do séptima mayor en segunda inversiónEn otro artículo presentaremos otras aplicaciones de la notación «barra» en las que la nota más grave puede incluso no pertenecer al acorde que matiza.
Es muy importante que incorpores las inversiones a tu repertorio de acordes. Por un lado, mantienen la cualidad del acorde pero suenan diferente y son, por lo tanto, un recurso más en tu paleta expresiva. Además, nos ayudan a dibujar melodías directamente sobre la progresión armónica, pues al usar deliberadamente las inversiones tenemos control de la disposición de las voces -particularmente de la más aguda y de la más grave.
Por otro lado, las inversiones permiten economía de movimientos, algo que saben muy bien los pianistas, que hacen uso intensivo de ellas. De este modo, las manos pueden encontrar el acorde destino buscando la inversión que esté más próxima al acorde de origen, no sólo minimizando así el salto necesario, sino facilitando una transición armónica más suave, tratando de mantener, en la medida de lo posible, las notas en común y persiguiendo el mínimo movimiento entre voces, uno de los principios de la continuidad armónica.
Javier Montero Gabarró
http://elclubdelautodidacta.es/wp/2015/07/inversion-de-acordes/
El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)
El Club del Autodidacta
Índice de todos los artículos de armonía.
Índice de lectura recomendado de la categoría Armonía.