Javier Montero | El Club del Autodidacta

Intervalos sin secretos: Ejercicios resueltos I

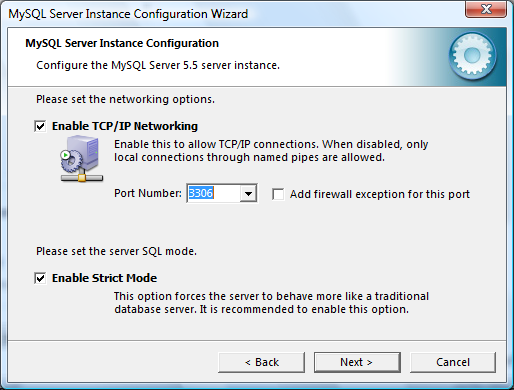
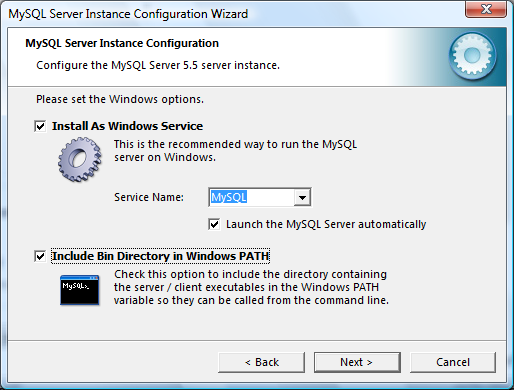
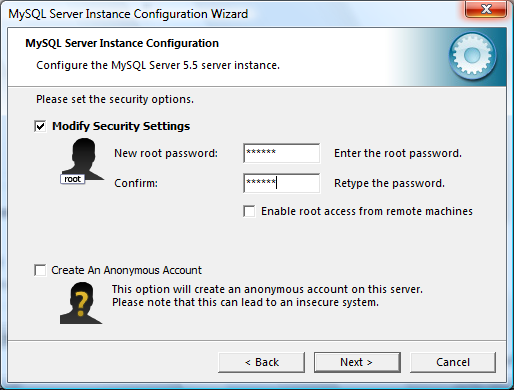
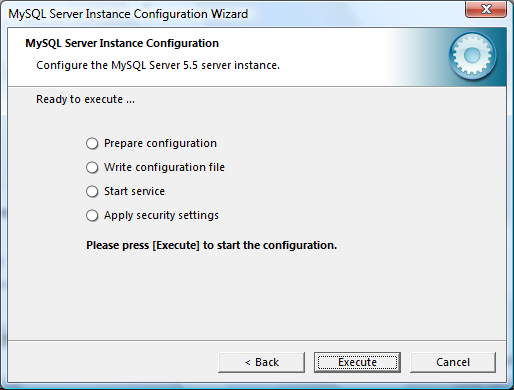
Vamos a dedicar un rato a aplicar lo aprendido sobre el cálculo de intervalos en los artículos anteriores (I y II) y resolveremos algunos ejercicios prácticos. En esta primera entrega trataremos algunos ejemplos básicos; en las próximas aplicaremos algunos métodos particulares y técnicas más avanzadas.

Para comprender estos ejercicios necesitamos remontarnos a la tabla de referencia que preparé hace unos días.

Ejercicio 1:

Los siguientes pares de notas delimitan un intervalo ascendente. Indicar de cuál se trata:

a) C – F#
b) A# – C
c) D – C
d) Gb – Db
e) Gb – D#

Solución:

a) Comenzamos calculando la distancia. Contamos sólo las notas naturales, incluyendo ambos extremos:

C – D – E – F

Se trata de una cuarta. Hay que determinar ahora su cualidad, para lo cual debemos contar el número de semitonos de diferencia totales:

C – C#(1) – D(2) – D#(3) – E (4) – F(5) – F#(6)

Seis semitonos (o tres tonos, tritono: el intervalo del diablo).

Consultamos la tabla y encontramos que dentro del grupo de cuartas, la que tiene seis semitonos es la aumentada.

Con lo que C – F# –> Cuarta aumentada

b) Determinemos la distancia:

A – B – C; una tercera.

Contemos semitonos:

A# – B(1) – C(2)

Miramos en la tabla el grupo de terceras y la que tiene dos semitonos es la disminuida:

A# – C –> Tercera disminuida

c) D – E – F – G – A – B – C; una séptima.

D – D#(1) – E(2) – F(3) – F#(4) – G(5) – G#(6) – A(7) – A#(8) – B(9) – C(10)

D – C –> Séptima menor

Más adelante veremos un modo mucho más rápido de llegar a esta conclusión, pero por el momento viene bien entretenerse con el conteo básico.

d) G – A – B – C – D; una quinta.

Gb – G(1) – G#(2) – A(3) – A#(4) – B(5) – C(6) – C#/Db(7) (observa que C# es enarmónico de Db)

Gb – Db –> Quinta justa o perfecta.

e) Al igual que el caso anterior, se trata de una quinta. Pero esta vez la distancia es 9 semitonos.

Gb – G(1) – G#(2) – A(3) – A#(4) – B(5) – C(6) – C#(7) – D(8) – D#(9)

La distancia de 9 semitonos no figura en el cuadro de quintas. ¿Qué intervalo es este?

Es un semitono más que el aumentado. A este tipo de intervalos se los conoce como doble aumentados.

De igual manera, al intervalo un semitono menor que el disminuido se le denomina doble disminuido.

Gb – D# –> Quinta doble aumentada

Date cuenta de que D# es enarmónico de Eb, por lo que, a efectos prácticos, una quinta doble aumentada es enarmónica de una sexta mayor.

Ningún misterio hasta aquí, ¿verdad? ¿Listo para el ejercicio 2?

Javier Montero Gabarró

Intervalos sin secretos: Ejercicios resueltos I

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

Fecha de la última modificación del artículo original: 30 de marzo de 2012

El Club del Autodidacta

A todos los suscriptores por correo electrónico

Una pequeña observación a todos los que recibís los artículos a través del correo eléctrónico: WordPress hace todo lo posible para que los los contenidos lleguen en las mejores condiciones de formato posible. Esto se logra en la mayor parte de los casos; no obstante, hay ocasiones en las que esto no sucede. En algunos artículos de temática relacionada con la programación se pueden observar algunas anomalías.

Esto es debido a que utilizo un plugin especial que me ayuda a preservar el código que incluyo en determinadas etiquetas, de modo que WordPress no lo interprete como HTML.

En particular, los artículos dedicados a la programación HTML hacen un uso intensivo del plugin. Si no fuera así, cada vez que escribiera código fuente (por ejemplo, ilustrando cómo crear una tabla en HTML), WordPress traduciría esas etiquetas y mostraría la tabla en lugar del código (que es lo que sucede en la edición por correo).

Sin embargo, me ha resultado muy curioso el comportamiento del sistema de correo cuando he tenido que introducir ecuaciones matemáticas, empleando un plugin de LaTeX que me proporciona un shortcode al efecto: la visualización de las fórmulas ha resultado perfecta.

Lo repito: casi siempre la visualización de los mensajes de correo será satisfactoria. No obstante, si no fuera el caso y detectáis algún tipo de anomalía, disculpad las molestias y no dudéis en visitar la página para recuperar la información en su mejor formato.

Javier Montero

Instalación de MySQL 5.5 para Windows

Hay varias razones por las que quizá te pueda interesar familiarizarte con el gestor de base de datos relacional MySQL. He aquí unas cuantas, por si alguna conecta contigo:

– Porque MySQL es la base de datos más instalada de todas. Es, con mucho, la reina de los servidores web, formando parte del trío imbatible AMP (Apache, MySQL y PHP).

– Porque es de código abierto y se ofrece bajo licencia GNU GPL.

– Porque eres desarrollador de aplicaciones web o de escritorio que trabajan con bases de datos y necesitas un entorno robusto.

– Porque necesitas gestionar tu productividad personal con bases de datos y no quieres pagar por algo que tienes gratis y mejor.

– Porque necesitas herramientas multiplataforma que no estén vinculadas con ningún sistema operativo o entorno particular.

– Porque quieres aprender SQL.

En otros artículos te he hablado de herramientas como WampServer que permiten una instalación local de Apache, PHP y MySQL. Instalar este tipo de herramientas 3 en 1 es una de las maneras con las que puedes disfrutar de MySQL.

Otra, objeto del artículo de hoy, es realizar la instalación independiente de MySQL. Concretamente, instalaremos MySQL 5.5 sobre un equipo con Windows. La instalación en otras plataformas es igual de sencilla, pero no será tratada en este momento.

Para descargarte MySQL debes dirigirte a la sección de descargas de la página oficial y elegir MySQL Community Server, que es la versión gratuita del producto. Selecciona Windows como plataforma y elige el instalador MSI que mejor se adapte a tu sistema operativo (32 o 64 bits).

El proceso de instalación es muy simple y prácticamente no requiere intervención por parte del usuario.

Comienza el proceso; sólo nos llevará un par de minutos…

Cada vez que veo la pantalla de la GNU GPL me lleno de felicidad. No sólo por las condiciones y el precio: es además, para mí, una garantía de profesionalidad.

Estadísticamente, la instalación típica será la que mejor se adapte a tus necesidades.

Todo listo; presiona Install cuando quieras.

Una vez instalado MySQL, la siguiente fase es la configuración del servidor en sí mismo. Asegúrate de que la marca Launch the MySQL Instance Configuration Wizard esté activa.

Adelante, sin miedo…

Optamos por Detailed Configuration, de modo que se optimice la configuración del servidor MySQL.

Ha llegado un momento crucial. Dependiendo del uso que vayamos a darle a nuestro servidor deberemos elegir una opción u otra, cada una con sus propios requerimientos de memoria. Puede que te guste la opción Developer Machine, para desarrolladores, la más apta para un uso de propósito general y la que menos recursos consume. Si vas a compartir servicios en esta máquina, probablemente Server Machine sea tu elección o, si vas a dedicarla exclusivamente como servidor SQL, puedes optar por Dedicated MySQL Server Machine, pues no te importará asignar la totalidad de los recursos a esta función.

De nuevo, para un uso de propósito general, te recomiendo la opción por defecto, Multifunctional Database.

InnoDB es el motor subyacente que dota de toda la potencia y seguridad a MySQL. Su funcionamiento requiere de unas tablas e índices cuya ubicación puedes configurar. Sin causas de fuerza mayor, acepta la opción por defecto.

Esta pantalla nos permite optimizar el funcionamiento del servidor en previsión del número de usos concurrentes. La opción por defecto, Decision Support (DSS) / OLAP será probablemente la que más te convenga.

Deja ambas opciones marcadas, tal como vienen por defecto. Es la más adecuada para un uso de propósito general o de aprendizaje, tanto si eres desarrollador como no. Aceptar conexiones TCP te permitirá conectarte al servidor desde otras máquinas (o desde la misma simulando un acceso web típico).

Hora de decidir qué codificación de caracteres emplearás. Salvo que quieras trabajar con Unicode porque necesites soporte multilenguaje, probablemente Latin1 te sirva (opción por defecto).

Instalamos MySQL como un servicio de Windows (la opción más limpia) y lo marcamos para que el motor de la base de datos arranque por defecto y esté siempre a nuestra disposición. La alternativa es hacer esto manualmente.

Además, me aseguro de marcar que los ejecutables estén en la variable PATH, para poder invocar a MySQL desde cualquier lugar en la línea de comandos.

Pon una contraseña al usuario root. Esto siempre es lo más seguro.

Si lo deseas, puedes indicar que el usuario root pueda acceder desde una máquina diferente a esta, aunque debo advertirte de que eso tal vez no sea una buena práctica de seguridad.

Última etapa: listos para generar el fichero de configuración y arrancar el servicio.

Se acabó… ¿Te esperabas algo más?

En las sucesivas entregas nos pondremos las pilas con MySQL, sea cual sea la plataforma que utilices.

Bienvenido a un viaje apasionante por el mundo de las bases de datos relacionales…

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2012/03/instalacion-de-mysql-5-5-para-windows/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

LaTeX – Capítulo 22: Aritmética básica

Una vez hemos visto cómo entrar en el modo matemático, estamos preparados para introducir ya notación propiamente dicha. Lo haremos muy gradualmente, presentando los distintos elementos matemáticos en pequeñas dosis prácticas.

Todo comienza con las operaciones aritméticas básicas: suma, resta, multiplicación y división.

$2+3=5$

Una verdad como pocas…

Para generar esto en LaTex introducimos la expresión así, tal cual:

\[
  2+3=5
\]

El uso de espacios en blanco en la expresión no contribuye a nada: LaTeX los elimina completamente y decide cuál ha de ser la presentación correcta. Este código tan espaciado no cambiaría en absoluto la forma del resultado:

\[
  x   +y =          z
\]

$x+y=z$

Veamos ahora el operador de resta y el signo negativo:

$2-3=-1$

\[
  2-3=-1
\]

El signo de multiplicación puede representarse de dos formas: mediante una equis o un punto. Para obtener estos símbolos disponemos de dos comandos: \times y \cdot, respectivamente. En inglés «tres por 2» se dice three times two; punto es dot, y cdot viene de centered dot, «punto centrado».

$2 \times 3=6$

\[
  2 \times 3 = 6
\]

$x \cdot y = z$

\[
  x \cdot y = z
\]

Después del nombre de un comando, como \cdot, sí que es necesario introducir un espacio en blanco. De lo contrario, LaTeX se pensaría que el comando es \cdoty y se produciría un error. Sin embargo, el siguiente código funcionaría bien:

\[
  2 \cdot3 = 6
\]

Esto es así porque un comando no puede terminar con un número. El último carácter alfabético determinaría el final del comando y no habría problema en su distinción.

Tenemos varias formas de realizar la división:

$6/3=2$

\[
  6/3=2
\]

o mediante los dos puntos:

$6:3=2$

\[
  6:3=2
\]

o, de un modo más elegante, con el comando \div:

$6 \div 3=2$

\[
   6 \div 3=2
\]

En la próxima entrega aprenderemos a introducir fracciones, no tengas prisa…

Los paréntesis se escriben tal cual, abriéndolos y cerrándolos tal como los encontramos:

$x(y+z)=xy+xz$

\[
  x(y+z)=xy+xz
\]

$(a+b) \cdot (c+d) = a \cdot c + a \cdot d + b \cdot c + b \cdot d$

\[
  (a+b) \cdot (c+d) = a \cdot c + a \cdot d + b \cdot c + b \cdot d
\]

Hay veces en las que necesitaremos emplear paréntesis más altos (por ejemplo, para contener fracciones). Veremos más adelante cómo insertar paréntesis que se adapten perfectamente a su contenido.

Nada más por hoy. Practica esta aritmética básica; coloca bien esta pequeña pieza del puzzle para que las demás encajen con facilidad.

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2012/03/latex-capitulo-22-aritmetica-basica/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

MuseScore #18: A veces oigo voces – I

Ha llegado el momento de acometer la escritura polifónica con MuseScore. Está claro que con las técnicas descritas hasta el momento no tenemos suficiente para escribir varias voces en un mismo pentagrama. Por un lado, escribir una segunda voz no es lo mismo que escribir un acorde, ya que en este caso todas las notas armónicas comparten la misma plica, algo no deseable en la representación polifónica.

Pero el principal inconveniente es que la escritura de acordes implica que todas las notas en el plano vertical deben tener la misma duración, lo cual no tiene por que ser así en la escritura de varias voces. Cuando sobre una nota añadimos otra de duración diferente nos encontramos que la nueva sobreescribe a la antigua, echándola a perder.

Son necesarias nuevas herramientas y las encontramos justo al final de la barra de Introducción de notas, en forma de un cuadrado con cuatro números de colores diferentes:

Comencemos por la tarea simple de escribir dos únicas voces. Las normas de la escritura polifónica nos dicen que la voz superior debe tener las plicas dirigidas hacia arriba y la inferior hacia abajo.

Por ejemplo, supongamos que deseamos escribir los dos siguientes compases:

Comenzamos escribiendo la voz superior empleando las técnicas que ya conocemos:

Observa que todas las notas sobre el Si van dirigidas, como es natural, con las plicas hacia abajo, mientras que las que están por debajo del Si las mantienen hacia arriba. Este es el comportamiento por defecto en la escritura monofónica.

Vamos a agregar ahora la segunda voz. Aprieta sobre el número 2, de color verde, en el cuadro de selección de voces de la primera figura.

Introduce la segunda voz. Observa como los cursores ahora aparecen de color verde, el propio de esta voz, mientras que el de la primera era el azul.

Como por arte de magia, las plicas de la primera voz que antes apuntaban hacia abajo han ido paulatínamente cambiándose solas conforme hemos introducido la segunda voz. No podía haber sido de otra manera.

En las próximas entradas profundizaremos gradualmente sobre el tema de las voces en MuseScore. Asegúrate de ir asimilando, hasta entonces, los rudimentos básicos.

PD: Entre el último artículo sobre MuseScore y este se ha liberado la versión 1.2 del programa, ultimo escalón hacia la ansiada versión 2.0. Si aún no te has actualizado, aprovecha el momento y hazlo ahora.

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2012/03/musescore-18-a-veces-oigo-voces-i/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

mIRC – Capítulo 20: Charlas moderadas

Ya conoces algunas maneras, como operador, para controlar el modo en que se accede a tu canal. Puedes ocultarlo haciéndolo invisible, protegerlo mediante contraseña o permitir la entrada exclusivamente por invitación. En el artículo de hoy veremos cómo moderar las conversaciones para que sólo aquellas personas que tengan la palabra puedan escribir en el canal en un momento dado.

Para que sostenuto, operador de #probilandia, convierta su canal en moderado, debe ejecutar el siguiente comando:

/mode #probilandia +m

Esto tiene el mismo efecto que activar la casilla Moderated en Channel Central:

Desde este preciso instante, a ningún miembro del canal le estará permitido escribir salvo que sostenuto le otorgue la voz.

El siguiente comando otorga la voz al usuario plutonio:

/mode #probilandia +v plutonio

Observa que, además del usuario al que se le da privilegios, es necesario indicar el nombre del canal.

Si ahora observas la lista de usuarios del canal verás que plutonio aparece precedido por un signo «+», indicando que tiene voz: +plutonio

Sostenuto puede otorgar voz a tantos usuarios como desee. La cuestión es que, en un momento dado, sólo podrán escribir aquellos que tengan privilegio para hacerlo.

Para retirar la voz a un usuario empleamos el modificador -v:

/mode #probilandia -v plutonio

Cuando sostenuto se canse de que su canal sea moderado, debe ejecutar:

/mode #probilandia -m

Con lo cual todos podrán hacer uso del canal de modo normal.

Hay una cosa más que debes saber: siendo operador puedes otorgar voces con +v aunque el canal no sea moderado. Al no estarlo, eso no tendrá ningún efecto a la hora de controlar quién habla, desde luego. Sin embargo, puedes utilizar de un modo creativo el signo «+» que precede a los usuarios con voz.

Por ejemplo, para establecer categorías de usuarios: además de los operadores, precedidos por una «@», puedes indicar un segundo nivel de jerarquía: la de aquellos que tienen un «+» delante suya.

O también puedes usar ese símbolo para diferenciar entre hombres y mujeres, algo que no siempre está del todo claro con el nick.

Imaginación al chat…

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2012/03/mirc-capitulo-20-charlas-moderadas/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Construcción de acordes – 10: novena añadida

Continuamos nuestro viaje por Acordilandia efectuando parada en el acorde de novena añadida y su delicioso sonido coloreando las triadas mayores.

Este acorde suele prestarse a confusión. ¿Por qué lo llamamos de novena añadida y no simplemente de novena? La razón es que este último es un acorde de dominante.

Existe un convenio por el que, cuando indicamos que un acorde es de novena, sobreentendemos la existencia de una séptima. Por lo tanto, un acorde de novena, así, a secas, es un acorde de séptima al que le agregamos una novena. Esto es: C9, Do novena, es realmente el acorde de séptima C7 más una novena. Para evitar confusiones muchos preferimos escribir este último acorde como C7(9). Volveremos con esto cuando le toque el turno a este tipo de acorde.

Regresemos a nuestra novena añadida. En cifrado moderno se indica agregando las letras add9 (add en inglés significa añadir) a la letra que representa al acorde.

Los acordes de novena añadida se construyen tomando una triada mayor y agregándole una nota más, la novena. Este acorde, a diferencia de C9, no lleva la séptima.

add9: 1 – 3 – 5 – 9

¿Qué nota es la novena? La que va después de la octava. Si, por ejemplo, estamos en la escala de Do mayor, la novena es un Re. Es decir, la novena es como la segunda, pero una octava más alta.

Si te has leído los últimos artículos que he escrito sobre intervalos ya sabrás que para saber qué nota es la equivalente cuando excedemos la octava, basta con restar siete.

Así, 9 – 7 = 2

Calculemos algunos acordes como ejemplo:

Do con novena añadida, Cadd9

Aplicamos el método descrito en esta serie, que comienza escribiendo la escala mayor:

C – D – E – F – G – A – B – C

Y cogemos los grados indicados en la fórmula (1 – 3 – 5 – 9)

Cadd9 –> C – E – G – D

Calculemos las notas de Aadd9:

La escala mayor de La es:

A – B – C# – D – E – F# – G# – A

con lo que:

Aadd9 –> A – C# – E – B

Si aún no conoces cómo suena este acorde en tu instrumento te sugiero que lo experimentes en lugar de alguna triada mayor simple. Su colorido es fascinante.

Javier Montero Gabarró

Construcción de acordes – 10: novena añadida

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

BitBite Python #2: Sumando las cifras

El camino hacia la pericia como programadores está plagado de ejercicios que van poniendo a prueba nuestra capacidad. Es absolutamente necesario pasar por ellos: resolviendo los problemas más elementales adquirimos las técnicas que nos permitirán afrontar los más complejos.

El programa de hoy es bien simple. Le pediremos al usuario que introduzca un número entero y nuestra misión será calcular la suma de todas sus cifras.

En el camino veremos cómo recorrer una cadena de caracteres (string) de principio a fin. Los strings son otro tipo de secuencias, como las tuplas o las listas y, como todas las secuencias, podemos acceder a sus elementos individualmente.

Comencemos solicitando la introducción del número y almacenando el dato en una variable:

numero=input('Introduce un número de las cifras que quieras: ')

Este tipo de sentencia ya te es familiar, pero no olvides que la entrada de input es una cadena de caracteres, aunque sólo hayamos introducido cifras numéricas. Es decir, la variable numero referencia a un string.

No estamos tratando, por el momento, los posibles errores de entrada. Confiamos en la buena fe del usuario, que sólo introducirá números.

Inicializamos la variable que contendrá la suma de todas las cifras:

suma=0

Vamos a recorrer ahora el string introducido desde el primer elemento hasta el último. Utilizaremos un bucle for:

for cifra in numero:
    suma+=int(cifra)

La variable cifra recorrerá uno a uno, todos los elementos de la secuencia (un string en este caso) de principio a fin. Por ejemplo, si numero es el string ‘207’, en la primera pasada del bucle, cifra es el carácter ‘2’, en la segunda ‘0’ y en la tercera ‘7’.

Date cuenta de que he rodeado cada cifra entre comillas. Esto es así porque los elementos de un array son caracteres simples, aunque representen un número.

Al ser caracteres simples y no números, para poder sumarlos necesitamos convertirlos a enteros. Para ello utilizamos la función int() que vemos en el bloque del for.

Una vez ha concluido el for tras recorrer todo el string, estamos en condiciones de imprimir el resultado final:

print(suma)

El programa sumacifras.py contiene el código completo de este sencillo ejercicio.

Javier Montero Gabarró

BitBite Python #2: Sumando las cifras

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Circuito Divina Pastora 2012 – Sevilla — Mejor marca personal

Este año, la edición sevillana del circuito Divina Pastora se ha adelantado respecto a las populares que organiza el IMD, que hasta el 22 de abril no iniciarán su andadura.

La carrera de hoy era una cita obligada. No sólo es la única prueba de 10K entre las que se celebran por aquí que está homologada por la federación de atletismo, sino que supuso mi mejor marca personal del año pasado en la distancia (54′ 10″, marca que me sirvió después para acreditar el cajetín sub55′ en la San Silvestre vallecana). Tengo el recuerdo de una organización excelente, un ambiente trepidante y un recorrido precioso bordeando el centro histórico sevillano. Y como no, compartiendo kilómetros con Fermín Cacho y Pentinel (con los que estuve, además, entrenando el día anterior a la prueba). Este año hemos contado con la participación estelar, además de Fermín, de Marta Domínguez, que justo ayer pulverizaba su marca de 10K en Laredo.

Llego 45 minutos antes de la salida al parque de María Luisa, desde donde comenzará y concluirá la carrera. Aparco la bicicleta y dejo mi ropa en el guardarropa. Es una mañana fresquita perfecta para correr.

Mi gran duda es a qué ritmo configuraré la liebre virtual del Forerunner para que tire de mí. Barajo tres posibilidades:

– 6’/Km, ritmo típico de mis entrenamientos.
– 5:45/Km, ritmo de los entrenamientos más exigentes
– 5:20, ritmo para intentar batir mi mejor marca personal

No termino de decidirme, por lo que aplazo la decisión hasta después del calentamiento en forma de unas cuantas vueltas alrededor de la Plaza de España.

Opto, finalmente, por configurar a ForeRundy a 5:45/Km, con lo que llegaría a meta en un máximo de 57 minutos y medio. Mi objetivo sería el de siempre, dejar atrás a FR tanto como me sea posible, pero con un compromiso adicional: no devolvería ni un solo metro de los ganados, es decir, mi ritmo instantáneo, en el peor de los casos, sería de 5:45/Km. En otras ocasiones me he permitido devolver metros con tal de no comprometer el objetivo final, pero esta vez no lo haría.

Arranco fuerte pero con excelentes sensaciones. He preferido dejar la cinta del pulsómetro en casa para no tener referencia de pulso cardíaco. Tampoco sé a qué ritmo ruedo: sólo utilizo una pantalla en la que se ve a mi compañero virtual y la distancia que nos separa en cada momento.

Se suceden los kilómetros y la distancia que le saco a ForeRundy se va contando en centenares de metros. Tan sólo en un momento me cuestiono si tal vez estoy rodando demasiado fuerte, pues hay un instante, antes de la mitad del recorrido, en el que me siento desfallecer y me veo obligado a disminuir algo la velocidad. Pero en poco segundos vuelvo a sentirme fuerte, recupero la concentración y aprieto otra vez.

Entro en meta en 52′ 23″, según el tiempo oficial. A mi compañero virtual le he sacado 900 metros y he pulverizado mi mejor marca personal en casi dos minutos.

He rodado 10 kilómetros a una media de 5:14/Km, algo que jamás habría imaginado ni en mis mejores pronósticos.

Contento y entero, ¿qué más se puede pedir?

Ahora, mientras llega la siguiente, retomar mis entrenamientos pacientes y lentos que tanto placer me dan.

Javier Montero Gabarró

http://elclubdelautodidacta.es/wp/2012/03/circuito-divina-pastora-2012-sevilla-mejor-marca-personal/

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Intervalos sin secretos: Tabla de Referencia y el Modelo del Muelle

En los dos artículos anteriores (primera parte y segunda parte) expliqué la teoría subyacente a la denominación de intervalos musicales. De cara a la resolución de los ejercicios prácticos, es conveniente reorganizar toda esta información agrupando los intervalos por la distancia entre sus grados (primera, segunda, tercera…).

Concluiremos con lo que denomino el modelo del muelle, que nos ayudará a afianzar todos estos conceptos con facilidad.

Tabla de referencia de intervalos

Primera
Justa o Perfecta: 0 semitonos
Aumentada: 1 semitono

Segunda
Disminuida: 0 semitonos
Menor: 1 semitono
Mayor: 2 semitonos
Aumentada: 3 semitonos

Tercera
Disminuida: 2 semitonos
Menor: 3 semitonos
Mayor: 4 semitonos
Aumentada: 5 semitonos

Cuarta
Disminuida: 4 semitonos
Justa o Perfecta: 5 semitonos
Aumentada: 6 semitonos

Quinta:
Disminuida: 6 semitonos
Justa o Perfecta: 7 semitonos
Aumentada: 8 semitonos

Sexta:
Disminuida: 7 semitonos
Menor: 8 semitonos
Mayor: 9 semitonos
Aumentada: 10 semitonos

Séptima:
Disminuida: 9 semitonos
Menor: 10 semitonos
Mayor: 11 semitonos
Aumentada: 12 semitonos

Octava:
Disminuida: 11 semitonos
Justa o Perfecta: 12 semitonos
Aumentada: 13 semitonos

Con esta sencilla tabla nos será muy sencillo resolver los ejercicios prácticos: comenzamos determinando la distancia entre las notas naturales para saber si se trata de una tercera, cuarta, etc., y contamos después el total de semitonos para aplicar la cualidad correspondiente.

El modelo del muelle

Visualiza un muelle normal. Puedes realizar dos tipos de acciones con él: estirarlo o comprimirlo.

Recuerda los intervalos que aparecían en la escala mayor desde la tónica hasta el resto: eran todos o bien justos o bien mayores. Tan sólo dos tipos.

Esos dos tipos de intervalos, justos y mayores, pueden ser representados por dos muelles. El hecho de estirar el muelle tendría el efecto de agregarle un semitono al intervalo; comprimirlo le restaría uno.

Comencemos por los muelles justos: si los estiramos los convertimos en aumentados; si los comprimimos en disminuidos.

Cojamos ahora el muelle mayor: si lo estiramos lo convertimos en aumentado, pero si lo comprimimos se convierte en menor. Esto nos permite tener la posibilidad de seguir comprimiéndolo todavía más: si lo aprieto un poco más (es decir, le quito otro semitono) se convierte ya en disminuido.

Los intervalos son como esos muelles: aumentar un semitono un intervalo justo o mayor los convierte en intervalos aumentados. Restar un semitono a un intervalo justo lo transforma en disminuido. Restar un semitono a un intervalo mayor lo hace menor y si a este, a su vez, le quitamos otro semitono lo convertimos finalmente en disminuido.

De este modo, no te hará falta memorizar la tabla entera. Por ejemplo, si te aprendes que una quinta justa son siete semitonos, sin necesidad de memorizar más sabrás ya que la quinta aumentada son ocho y la disminuida seis. Si sabes que una séptima mayor son once semitonos, tienes inmediatamente que la aumentada son doce, la menor diez y la disminuida nueve.

Javier Montero Gabarró

Intervalos sin secretos: Tabla de Referencia y el Modelo del Muelle

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Autor: Javier Montero

Intervalos sin secretos: Ejercicios resueltos I

Ejercicio 1:

Solución:

A todos los suscriptores por correo electrónico

Instalación de MySQL 5.5 para Windows

LaTeX – Capítulo 22: Aritmética básica

MuseScore #18: A veces oigo voces – I

mIRC – Capítulo 20: Charlas moderadas

Construcción de acordes – 10: novena añadida

BitBite Python #2: Sumando las cifras

Circuito Divina Pastora 2012 – Sevilla — Mejor marca personal

Intervalos sin secretos: Tabla de Referencia y el Modelo del Muelle

Tabla de referencia de intervalos

El modelo del muelle

Uso de cookies

Ejercicio 1:

Solución:

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tal vez te interese...

Tabla de referencia de intervalos

El modelo del muelle

Tal vez te interese...

Uso de cookies