Objetivo: presentar con más profundidad los comandos que permiten crear cajas horizontales en LaTeX.
Objetivo: presentar con más profundidad los comandos que permiten crear cajas horizontales en LaTeX.
En el artículo anterior introdujimos el modo LR y mostramos el comando mbox, que activaba ese modo para la creación de una sencilla caja horizontal. Hoy profundizaremos presentando unos comandos que nos permitirán unos diseños más avanzados.
Si recuerdas, mbox es un sastre que crea un traje perfectamente a medida, una caja adaptada rigusoramente al texto que se especifica como parámetro. Pero es un traje invisible: en el resultado final puede que ni siquiera seamos capaz de diferenciar la existencia de la caja. Y es que el comando mbox cumple su misión sin necesidad de llamar la atención.
Para hacer visible nuestra caja LR, LaTeX nos ofrece el comando fbox que, al igual que mbox, crea una contenedor del tamaño exacto del texto, pero con la particularidad de que aparecece encuadrado en un marco.
\documentclass{article}
\usepackage[spanish]{babel}
\usepackage[utf8]{inputenc}
\usepackage{parskip}
\begin{document}
Si eres músico, es importante que, de cuando en cuando,
acudas al otorrinolaringólogo a revisar tu audición.
Si eres músico, es importante que, de cuando en cuando,
acudas al \mbox{otorrinolaringólogo} a revisar tu audición.
Si eres músico, es importante que, de cuando en cuando,
acudas al \fbox{otorrinolaringólogo} a revisar tu audición.
\end{document}
En el primer párrafo, la palabra otorrinolaringólogo está escrita con normalidad, sin caja, permitiendo a LaTeX dividirla, como sucede en el ejemplo, para una mejor presentación. En los párrafos segundo y tercero se enmarca con mbox y fbox, respectivamente, preservando su longitud total y evitando así su división.
Es posible también arreglar el traje y no cortarlo necesariamente a medida, sino a la longitud que queramos, aún pudiéndonos quedar paticortos o con los bajos arrastrando por el suelo.
El comando makebox es una variante de mbox que permite crear una caja de la anchura especificada, pudiendo indicar, además, el tipo de justificación que tendrá el texto dentro de ella:
\makebox[anchura][justificación]{texto}
Observa, por el corchete, que tanto anchura como justificación son opcionales.
En el parámetro anchura introducimos una medida de longitud (es importante no olvidar las unidades junto al valor numérico). En justificación podemos indicar l, r o c para expresar justificación izquierda (l), derecha (r) o centrado (c). El valor por omisión, si no se indica nada, es c, apareciendo el texto centrado en la caja.
Un ejemplo nos ayudará a entenderlo mejor:
\begin{document}
Ya no echan series como \mbox{La casa de la pradera},
es una verdadera lástima.
Ya no echan series como \makebox[6cm][c]{La casa de la pradera},
es una verdadera lástima.
Ya no echan series como \makebox[6cm][l]{La casa de la pradera},
es una verdadera lástima.
Ya no echan series como \makebox[6cm][r]{La casa de la pradera},
es una verdadera lástima.
\end{document}El primer párrafo hace uso de mbox, ajustando la caja a la medida del texto. En los siguientes establecemos una anchura de 6 cm, observando su justificación centrada, izquierda o derecha.
La caja creada tiene anchura suficiente para acoger el texto que contiene, pero podría darse el caso de que no. Observa qué sucede si el traje se nos queda corto:
\begin{document}
Ya no echan series como \makebox[2cm][c]{La casa de la pradera},
es una verdadera lástima.
Ya no echan series como \makebox[2cm][l]{La casa de la pradera},
es una verdadera lástima.
Ya no echan series como \makebox[2cm][r]{La casa de la pradera},
es una verdadera lástima.
\end{document}La caja tiene una anchura de 2cm, quepa o no quepa su contenido en ella. LaTeX la considera como si de un único carácter se tratase, escribiendo el siguiente justo a continuación de la caja, lo que explica la superposición de texto.
Naturalmente, al igual que sucedía con mbox, el comando makebox tiene su versión con marco: framebox.
\begin{document}
Ya no echan series como \framebox[6cm][c]{La casa de la pradera},
es una verdadera lástima.
Ya no echan series como \framebox[6cm][l]{La casa de la pradera},
es una verdadera lástima.
Ya no echan series como \framebox[6cm][r]{La casa de la pradera},
es una verdadera lástima.
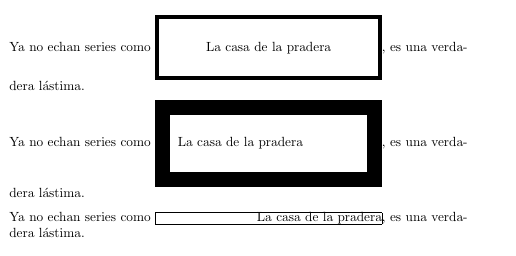
\end{document}Para finalizar, si eres un usuario de LaTeX inquieto debes saber qué hay dos longitudes que permiten controlar la estética de estas cajas. Puedes regular el ancho del marco con fboxrule y su separación del texto con fboxsep. Al igual que otras longitudes LaTeX, su valor se establece con el comando setlength, del que creo haber hablado ya en alguna que otra ocasión.
\begin{document}
\setlength{\fboxrule}{1mm}
\setlength{\fboxsep}{6mm}
Ya no echan series como \framebox[6cm][c]{La casa de la pradera},
es una verdadera lástima.
\setlength{\fboxrule}{4mm}
\setlength{\fboxsep}{6mm}
Ya no echan series como \framebox[6cm][l]{La casa de la pradera},
es una verdadera lástima.
\setlength{\fboxrule}{.1mm}
\setlength{\fboxsep}{0mm}
Ya no echan series como \framebox[6cm][r]{La casa de la pradera},
es una verdadera lástima.
\end{document}Fíjate en el último ejemplo, con un parámetro de separación nulo (aunque sea cero es preceptivo el uso de unidades): el marco aparece ajustado al límite más alto y bajo de los caracteres contenidos (letras L y p).
A lo largo de los años que llevo trabajando con LaTeX nunca he dejado de aprender, se trate de un comando nativo o de uno englobado en un paquete que extiende su funcionalidad. Cuidadosamente, he ido construyendo mi propio manual de referencia con cada pieza que he ido encontrando en el camino. El universo LaTeX es casi inconmensurable y recomiendo encarecidamente que hagas lo mismo. Si las cajitas de este artículo no forman parte aún de tu repertorio de técnicas, toma buena nota de ellas.
Javier Montero Gabarró
El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)
El Club del Autodidacta
Índice completo de artículos relacionados con .