Objetivo: desarrollar en la guitarra la escala de tonos enteros en formas libres.
Objetivo: desarrollar en la guitarra la escala de tonos enteros en formas libres.
En el anterior artículo de esta serie ilustramos la forma de producir en la guitarra el intervalo de tono, equivalente a una segunda mayor. Estudiamos su formación en la misma cuerda o saltando a la adyacente.
Vamos a poner en práctica este conocimiento aplicándolo a una escala muy concreta en cuya construcción sólo interviene el intervalo de tono: la escala de tonos enteros, explicada en este blog dentro de la categoría Armonía.
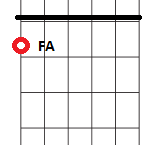
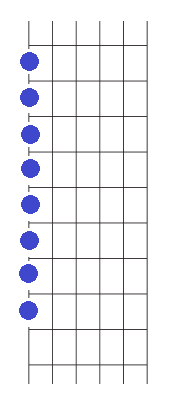
Elijamos de partida una nota cualquiera. Por ejemplo, el FA existente en el primer traste de la sexta cuerda:
La siguiente nota de la escala, SOL, está a un tono de ella. Es decir, subimos dos trastes más, aterrizando en el tercer traste:
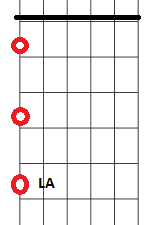
Para realizar el siguiente tono, LA, se nos ofrecen dos caminos posibles: seguir subiendo por la misma cuerda o saltar a la quinta. Como somos libres, elegimos el que más nos plazca:
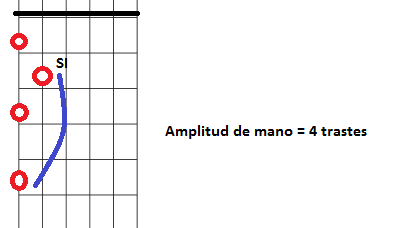
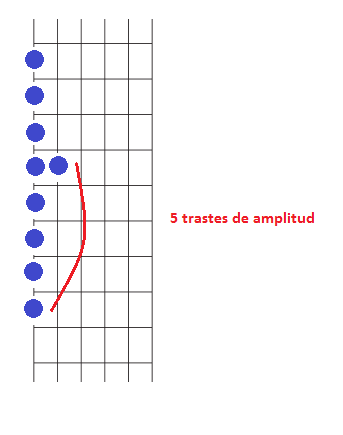
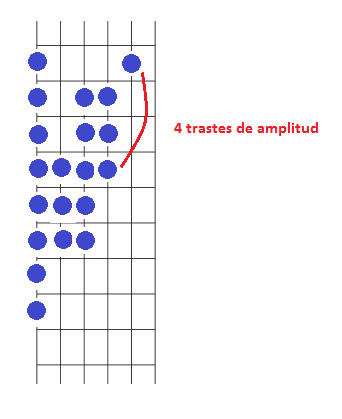
El siguiente tono, SI, lo vamos a hacer sonar en la quinta cuerda. Recordemos que para ello damos un salto hacia atrás sobre la siguiente cuerda con una amplitud completa de 4 trastes.
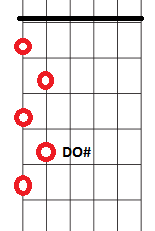
DO# lo tomamos subiendo por la misma cuerda. Observa que estamos demasiado cerca del clavijero como para poder dar un salto hacia atrás hacia la cuarta cuerda.
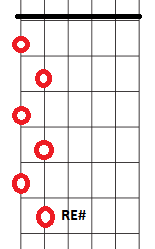
Para el RE# se nos abren, nuevamente, dos posibilidades. Por ejemplo:
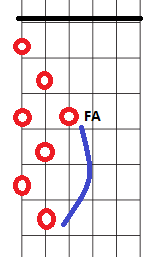
El siguiente grado de la escala de tonos enteros, FA, lo vamos a producir saltando de cuerda:
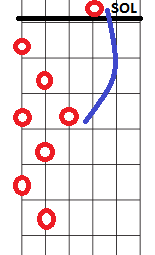
Completando así la primera octava de la escala. Comenzamos la siguiente con un salto a la tercera cuerda. Observa que esta vez aterrizamos sobre el SOL al aire.
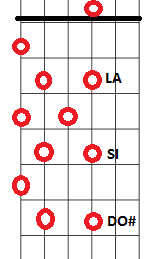
Y ahora proseguimos, por ejemplo, con tres apoyos sobre la misma cuerda:
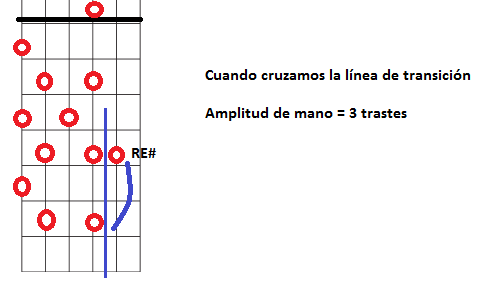
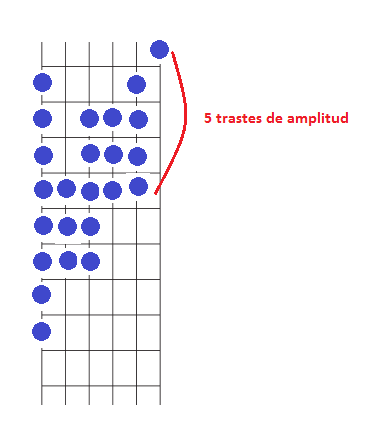
Muy atento ahora porque vamos a cruzar la línea de transición imaginaria que separa la tercera y la segunda cuerda, que ya sabes se afinan de forma diferente respecto a los demás pares. Cuando cruzamos esa línea el salto de tono tiene una amplitud de tres trastes, y no de cuatro:
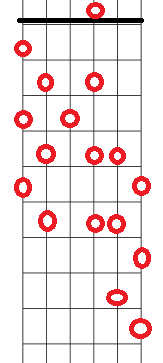
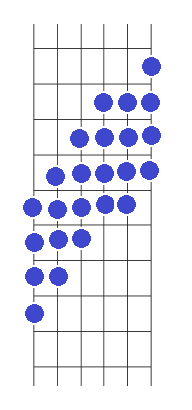
Lo que resta no merece explicación. Por ejemplo, podríamos recorrer la escala así:
Coge la guitarra y realiza tu mismo esto que he hecho yo, pera esta vez escogiendo tu propia ruta.
¿Fácil? Traza ahora el camino inverso, recorriendo la escala descendentemente. Es muy importante que te acostumbres a saltar tanto hacia adelante como hacia atrás.
Vuelve otra vez a la escala de tonos enteros ascendente, pero esta vez comenzando un semitono más adelante que donde empezamos la otra vez. Es decir, crea la escala partiendo del FA# que hay en el segundo traste de la sexta cuerda.
Cuando termines, repite la operación otro semitono más adelante aún, es decir, comenzando ahora en SOL (tercer traste de la sexta cuerda).
¿Encuentras alguna particularidad?
Las notas de la escala de tonos enteros, al empezar en SOL, son las mismas que cuando lo hacíamos en FA:
FA tonos enteros: FA – SOL – LA – SI – DO# – RE# – FA …
SOL tonos enteros: SOL – LA – SI – DO# – RE# – FA – SOL …
Quizás creas que, aunque sean las mismas notas, se trata de escalas distintas, al igual que sucede con los modos griegos. Pues no; es exactamente la misma escala. Los modos griegos, aunque comparten las mismas notas, se diferencian en la composición interválica entre grado y grado (es decir, cada modo tiene su propia fórmula). En cambio, en la escala de tonos enteros hay exactamente la misma distancia interválica entre grado y grado: el constante TONO.
Si te has leído el artículo de la sección de armonía esta conclusión no debería sorprenderte: ¡sólo hay dos escalas de tonos enteros posibles! La escala de FA es la misma que la de SOL, LA, SI, DO# y RE#, al igual que la escala de FA# es la misma que la de SOL#, LA#, DO, RE y MI.
Lo explicado hoy guarda una relación estrecha con el artículo que dedicamos a la escala cromática en libertad, publicado una vez ilustramos el intervalo de semitono. El propósito no es otro sino adquirir las habilidades básicas necesarias para la elaboración de escalas un poco más complejas. En el próximo aplicaremos estos conceptos para la construcción libre de la escala diatónica por excelencia: la escala mayor.
Javier Montero Gabarró
El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)
El Club del Autodidacta