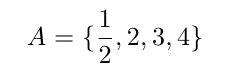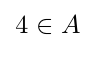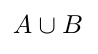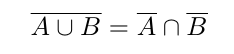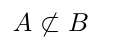subconjuntos | El Club del Autodidacta

Objetivo: aprender a generar en LaTeX la simbología relacionada con los conjuntos matemáticos.

Hace tan sólo dos días escribía un artículo sobre programación en Python relacionado con los conjuntos y caí en la cuenta de que aún no había mencionado nada sobre ellos en $\LaTeX$ . No es la primera vez que aprovecho una misma temática para enfocarla bajo la luz de distintas disciplinas (como las listas en Python, en LaTeX o en HTML). De modo que quiero compartir hoy contigo lo que sé sobre notación de conjuntos en LaTeX, es decir, mostrarte cómo pintar esos simbolitos de unión, intersección, pertenencia, etc.

Comencemos describiendo los elementos que definen un conjunto:

La única pega que tiene esto es la generación de las llaves, pues sabes que son un símbolo reservado de $\LaTeX$ .

Para poder escribir las llaves, debes escaparlas con \{ y \}, de modo que el código que genera la imagen de la figura es el siguiente:

\[
A=\{1, 2, 3, 4\}
\]

Pero esto puede suponer un problema, al igual que sucedía con los paréntesis: si el contenido presenta varias alturas, las llaves se quedarán pequeñas. Obsérvalo en la siguiente imagen:

De modo que toma nota del comando inteligente para generar llaves: \left\{ para la llave de apertura y \right\} para la de cierre. Ahora está mucho mejor:

\[
A=\left\{\frac{1}{2}, 2, 3, 4\right\}
\]

Comprendido esto, continuemos con la pertenencia:

Los comandos para indicar pertenencia o no pertenencia son \in y \notin, respectivamente:

\[
4 \in A
\]

\[
5 \notin A
\]

Voy a explicarte otra forma más de generar el símbolo de no pertenencia y que aplicaremos después para la forma negada del operador de inclusión. Basta con que precedas el operador a negar con el comando \not. Obsérvalo:

\[
5 \not \in A
\]

El resultado es exactamente el mismo.

Para la unión e intersección disponemos de los comandos \cup y \cap, respectivamente. La elección de estos términos no es arbitraria: cup significa taza en inglés, que es como la U de la unión. En cambio, cap significa gorro, un objeto que podemos asimilar fácilmente a la U invertida de la intersección.

\[
A \cup B
\]

\[
A \cap B
\]

Si te gusta indicar el complementario de un conjunto con una barra horizontal, toma nota del comando \overline, que dibujará una línea horizontal sobre aquello que facilites como argumento entre llaves. Por ejemplo, para generar la siguiente ley de Morgan

habría que escribir el siguiente código:

\[
\overline{A \cup B}=\overline{A} \cap \overline{B}
\]

El símbolo de inclusión, contenido en, lo creamos a través del comando \subset (subconjunto). Su variante, contiene a, se logra con \supset (superconjunto).

\[
A \subset B
\]

\[
B \supset A
\]

Si agregas eq, de equal, al final de estos comandos, obtienes la versión con igualdad:

\[
A \subseteq B
\]

\[
B \supseteq A
\]

Para el no incluido y el no contiene, precedemos el comando con \not, de igual modo que hicimos con la no pertenencia. Observa estos dos ejemplos:

\[
A \not \subset B
\]

\[
B \not \supseteq A
\]

Lo he soltado, ya me he quedado más a gusto…

Javier Montero Gabarró

LaTeX: Notación relacionada con los conjuntos

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Índice completo de artículos relacionados con $\LaTeX$ .

Objetivo: implementar los conceptos de subconjuntos y conjuntos disjuntos en Python.

Vamos a ir concluyendo el tema de los conjuntos, que tengo interés en presentar pronto otra de las superestructuras fabulosas de Python, los diccionarios.

La teoría nos dice que A es subconjunto de B cuando A está incluido en B, que es lo mismo que decir que B contiene a A.

Para implementar estos conceptos en Python, disponemos de los operadores de comparación habituales:

== igual
!= distinto
>  mayor
>= mayor o igual
<  menor
<= menor o igual

A es un subconjunto de B cuando todos los elementos de A están incluidos en B, relación que expresamos por

A <= B

que es equivalente a

B >= A

Puede interesarte también la inclusión estricta:

A < B, que es lo mismo que decir B > A

Practiquemos estos operadores con los siguientes conjuntos:

>>> c1 = {1, 2, 3}
>>> c2 = {1, 2, 3}
>>> c3 = {1, 2, 3, 4, 5, 6}
>>> c4 = {2, 4, 6}
>>> c5 = {1, 3, 5}

Observa que c1 y c2 son iguales, pues contienen los mismos elementos

>>> c1 == c2
True

pero c2 y c3 no lo son:

>>> c2 != c3
True

Sin embargo, c2 es un subconjunto de c3, pues todos los elementos de aquel están incluidos en este:

>>> c2 <= c3
True

A su vez, c1 es un subconjunto de c2, aunque sean iguales:

>>> c1 <= c2
True

Pero no lo sería en sentido estricto:

>>> c1 < c2
False

El concepto de subconjunto también está disponible como método:

>>> c1.issubset(c3)
True

que debe leerse como c1 es subconjunto de c3,

y es lo mismo que

c1 <= c3

También puedes expresarlo del siguiente modo:

>>> c3.issuperset(c1)
True

que debes leerlo como c3 es superconjunto de c1, que es lo mismo que decir que c3 contiene a c1:

c3 >= c1

Para finalizar, unas palabras sobre el concepto de conjuntos disjuntos. Sabemos que dos conjuntos son disjuntos cuando no tienen elementos en común, es decir, su intersección es el conjunto vacío.

En el artículo anterior tratamos la intersección, así que ya tenemos recursos para practicar esto sobre los conjuntos c4 y c5, que como puedes observar, son disjuntos:

>>> c4 & c5 == set()
True

Recuerda que set() simboliza el conjunto vacío, y no {}, que sería un diccionario vacío, como veremos muy pronto.

Pero esta instrucción podría prestarse a error fácilmente: el uso de set() o el orden de evaluación de los operadores.

¿Qué tal esta otra, más sencilla?

>>> c4.isdisjoint(c5)
True

Se acerca el final del repaso que le estamos dando a los conjuntos en Python. En la próxima entrega presentaremos el tipo frozenset, conjunto congelado, que es como el tipo set, pero inmutable.

Qué trascendente ha sonado esta última palabra; me está entrando hasta frío…

Javier Montero Gabarró

Python: Subconjuntos – Conjuntos disjuntos

El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)

El Club del Autodidacta

Consulta el índice completo de artículos relacionados con Python.

Etiqueta: subconjuntos

LaTeX: Notación relacionada con los conjuntos

Python: Subconjuntos – Conjuntos disjuntos

Uso de cookies

Tal vez te interese...

Tal vez te interese...

Uso de cookies