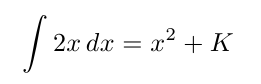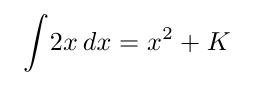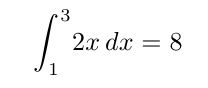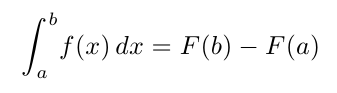Objetivo: aprender a generar el símbolo de integral en LaTeX y mostrar cómo definir los límites superior e inferior.
Objetivo: aprender a generar el símbolo de integral en LaTeX y mostrar cómo definir los límites superior e inferior.
Me siento hoy con ganas de dar una nueva incursión en el modo matemático de , hace ya unos cuantos días desde la última vez. A lo largo de esta serie hemos presentado bastantes elementos de la faceta matemática de
, pero aún quedan muchos actores por entrar esta escena.
Ladies and gentlemen, señoras y señores, con todos vosotros, la agraciada y presumida integral.
Escribir una integral es tan simple como ejecutar el comando \int. Observa la siguiente instrucción:
\[
\int 2x dx = x^{2}
\]que genera esta salida:
Ahí la tenemos, tan altiva y orgullosa.
No obstante, a poco que observes el resultado apreciarás unas consideraciones relacionadas con el diseño que podríamos mejorar. Observa que el dx está demasiado cerca del 2x.
Para separar dx de la función dispone del comando
\, (la barra inclinada y una coma), que sirve para añadir un pequeño espacio.
Observa la nueva versión mejorada:
\[
\int 2x \, dx = x^{2}+K
\]Esto ya es otra cosa.
Hay gente que afina más aún y prefiere acercar el símbolo de la integral al comienzo de la función. Para lograr esto disponemos del comando \! que inserta un pequeño espacio negativo (hacia atrás).
\[
\int \! 2x \, dx = x^{2}+K
\]Nuestra afortunada integral a menudo se deja ver con dos lujosos pendientes en forma de límite superior e inferior. Para generarlos recurrimos a los socorridos subíndices y superíndices, que tanto buen apaño nos han dado ya.
Establecemos el límite inferior de la integral mediante notación subíndice y el superior con superíndice.
\[
\int_{1}^{3} \! 2x \, dx = 8
\]Hemos aplicado la conocida regla de Barrow del cálculo integral, por la que seguro habrás pasado alguna que otra vez en tus tiempos de estudiante, si te ha llamado la atención el artículo tanto como para leer hasta aquí.
\[
\int_{a}^{b} \! f(x) \,dx = F(b) - F(a)
\]en la que f(x) es una función continua en el intervalo [a, b] y F(x) es su primitiva.
Javier Montero Gabarró
Fecha de última modificación: 9 de agosto de 2012
El texto de este artículo se encuentra sometido a una licencia Creative Commons del tipo CC-BY-NC-ND (reconocimiento, no comercial, sin obra derivada, 3.0 unported)
El Club del Autodidacta
Índice completo de artículos relacionados con .